1A Probability extension problems

Aside

This year, I was lecturing the first year probability course in Cambridge. To supplement the usual excellent problem sets I inherited from James Norris and many previous lecturers, I prepared extension problems for enthusiastic students. A handful of the extension problems are original; a few are simplifications or examples of problems in graduate-level discrete probability. The first sheet is more gentle than the subsequent three.

These can be found below.

Cambridge_extension_Problems Download

Cambridge supervisors are welcome to use these in subsequent years. Indeed, anyone is welcome to use these in their teaching. Solutions are available for instructors – please contact me by email to receive these.

EGMO 2016 Paper I

Posted on April 13, 2016 by dominicyeo

We’ve just our annual selection and training camp for the UK IMO team in Cambridge, and I hope it was enjoyed by all. I allotted myself the ‘graveyard slot’ at 5pm on the final afternoon (incidentally, right in the middle of this, but what England fan could have seen that coming in advance?) and talked about random walks on graphs and the (discrete) heat equation. More on that soon perhaps.

The UK has a team competing in the 5th European Girls Mathematical Olympiad (hereafter EGMO 2016) right now in Busteni, Romania. The first paper was sat yesterday, and the second paper is being sat as I write this. Although we’ve already sent a team to the Romania this year (where they did rather well indeed! I blame the fact that I wasn’t there.), this feels like the start of the olympiad ‘season’. It also coincides well with Oxford holidays, when, though thesis deadlines loom, I have a bit more free time for thinking about these problems. Anyway, last year I wrote a summary of my thoughts and motivations when trying the EGMO problems, and this seemed to go down well, so I’m doing the same this year. My aim is not to offer official solutions, or even outlines of good solutions, but rather to talk about ideas, and how and why I decided whether they did or didn’t work. I hope some of it is interesting.

You can find the paper in many languages on the EGMO 2016 website. I have several things to say about the geometry Q2, but I have neither enough time nor geometric diagram software this morning, so will only talk about questions 1 and 3. If you are reading this with the intention of trying the problems yourself at some point, you probably shouldn’t keep reading, in the nicest possible way.

Question 1

[Slightly paraphrased] Let n be an odd positive integer and $x_1,\ldots,x_n\ge 0$ . Show that

$\min_{i\in[n]} \left( x_i^2+x_{i+1}^2\right) \le \max_{j\in[n]} 2x_jx_{j+1},$

where we define $x_{n+1}=x_1$ cyclically in the natural way.

Thought 1: this is a very nice statement. Obviously when i and j are equal, the inequality holds the other way round, and so it’s interesting and surprising that constructing a set of pairs of inequalities in the way suggested gives a situation where the ‘maximum minimum’ is at least the ‘minimum maximum’.

Thought 2: what happens if n is actually even? Well, you can kill the right-hand-side by taking at least every other term to be zero. And if n is even, you really can take every other term to be even, while leaving the remaining terms positive. So then the RHS is zero and the LHS is positive.

The extension to this thought is that the statement is in danger of not holding if there’s a lot of alternating behaviour. Maybe we’ll use that later.

Idea 1: We can write

$2(x_i^2+x_{i+1}^2)=(x_i+x_{i+1})^2 + |x_i-x_{i+1}|^2, \quad 4x_ix_{i+1}=(x_i+x_{i+1})^2 - |x_i-x_{i+1}|^2,$

which gives insight into ‘the problem multiplied by 2’. This was an ‘olympiad experience’ idea. These transformations between various expressions involving sums of squares turn out to be useful all the time. Cf BMO2 2016 question 4, and probably about a million other examples. As soon as you see these expressions, your antennae start twitching. Like when you notice a non-trivial parallelogram in a geometry problem, but I digress. I’m not sure why I stuck in the absolute value signs.

This was definitely a good idea, but I couldn’t find a way to make useful deductions from it especially easily. I tried converting the RHS expression for i (where LHS attains minimum) into the RHS expression for any j by adding on terms, but I couldn’t think of a good way to get any control over these terms, so I moved on.

Idea 2: An equality case is when they are all equal. I didn’t investigate very carefully at this point whether this might be the only equality case. I started thinking about what happens if you start with an ‘equal-ish’ sequence where the inequality holds, then fiddle with one of the values. If you adjust exactly one value, then both sides might stay constant. It seemed quite unlikely that both would vary, but I didn’t really follow this up. In any case, I didn’t feel like I had very good control over the behaviour of the two sides if I started from equality and built up to the general case by adjusting individual values. Or at least, I didn’t have a good idea for a natural ordering to do this adjustment so that I would have good control.

Idea 3: Now I thought about focusing on where the LHS attains this minimum. Somewhere, there are values (x,y) next to each other such that 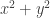$x^2+y^2$ is minimal. Let’s say 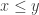$x\le y$ . Therefore we know that the element before x is at least y, and vice versa, ie we have

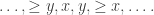
$\ldots, \ge y, x, y, \ge x,\ldots.$

and this wasn’t helpful, because I couldn’t take this deduction one step further on the right. However, once you have declared the minimum of the LHS, you are free to make all the other values of $x_i$ smaller, so long as they don’t break this minimum. Why? Because the LHS stays the same, and the RHS gets smaller. So if you can prove the statement after doing this, then the statement was also true before doing this. 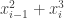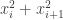So after thinking briefly, this means that you can say that for every i, either $x_{i-1}^2+x_i^3$ or $x_i^2+x_{i+1}^2$ attains this minimum.

Suddenly this feels great, because once we know at least one of the pairs corresponding to i attains the minimum, this is related to parity of n, which is in the statement. At this point, I was pretty confident I was done. Because you can’t partition odd [n] into pairs, there must be some i which achieves a minimum on both sides. So focus on that.

Let’s say the values are (x,y,x) with 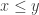$x\le y$ . Now when we try to extend in both directions, we actually can do this, because the values alternate with bounds in the right way. This key is to use the fact that the minimum 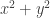$x^2+y^2$ must be attained at least every other pair. (*) So we get

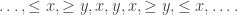
$\ldots, \le x,\ge y,x,y,x,\ge y,\le x,\ldots.$

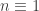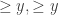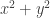But it’s cyclic, so the ‘ends’ of this sequence join up. If $n\equiv 1$ modulo 4, we get $\ge y,\ge y$ next to each other, which means the RHS of the statement is indeed at least the LHS. If $n\equiv 3$ modulo 4, then we get $\le x,\le x$ next to each other, which contradicts minimality of $x^2+y^2$ unless x=y. Then we chase equality cases through the argument (*) and find that they must all be equal. So (after checking that the case 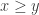$x\ge y$ really is the same), we are done.

Thought 3: This really is the alternating thought 2 in action. I should have probably stayed with the idea a bit longer, but this plan of reducing values so that equality was achieved often came naturally out of the other ideas.

Thought 4: If I had to do this as an official solution, I imagine one can convert this into a proof by contradiction and it might be slightly easier, or at least easier to follow. If you go for contradiction, you are forcing local alternating behaviour, and should be able to derive a contradiction when your terms match up without having to start by adjusting them to achieve equality everywhere.

Question 3

Let m be a positive integer. Consider a 4m x 4m grid, where two cells are related to each other if they are different but share a row or a column. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.

Thought 1: I spent the majority of my time on this problem working with the idea that the answer was 8m. Achieved by taking two in each row or column in pretty much any fashion, eg both diagonals. This made me uneasy because the construction didn’t take advantage of the fact that the grid size was divisible by 4. I also couldn’t prove it.

Thought 2: bipartite graphs are sometimes useful to describe grid problems. Edges correspond to cells and each vertex set to row labels or column labels.

Idea 1: As part of an attempt to find a proof, I was thinking about convexity, and why having exactly two in every row was best, so I wrote down the following:

Claim A: No point having three in a row.

Claim B: Suppose a row has only one in it + previous claim => contradiction.

In Cambridge, as usual I organised a fairly comprehensive discussion of how to write up solutions to olympiad problems. The leading-order piece of advice is to separate your argument into small pieces, which you might choose to describe as lemmas or claims, or just separate implicitly by spacing. This is useful if you have to do an uninteresting calculation in the middle of a proof and don’t want anyone to get distracted, but mostly it’s useful for the reader because it gives an outline of your argument.

My attempt at this problem illustrates an example of the benefit of doing this even in rough. If your claim is a precise statement, then that’s a prompt to go back and separately decide whether it is actually true or not. I couldn’t prove it, so started thinking about whether it was true.

Idea 2: Claim A is probably false. This was based on my previous intuition, and the fact that I couldn’t prove it or get any handle on why it might be true. I’d already tried the case m=1, but I decided I must have done it wrong so tried it again. I had got it wrong, because 6 is possible, and it wasn’t hard from here (now being quite familiar with the problem) to turn this into a construction for 6m in the general case.

Idea 3: This will be proved by some sort of double-counting argument. Sometimes these arguments turn on a convexity approach, but when the idea is that a few rows have three blue cells, and the rest have one, this now seemed unlikely.

Subthought: Does it make sense for a row to have more than three blue cells? No. Why not? Note that as soon as we have three in a row, all the cells in that row are fine, irrespective of the rest of the grid. If we do the problem the other way round, and have some blues, and want to fill out legally the largest possible board, why would we put six in one row, when we could add an extra row, have three in each (maintaining column structure) and be better off than we were before. A meta-subthought is that this will be impossible to turn into an argument, but we should try to use it to inform our setup.

Ages and ages ago, I’d noticed that you could permute the rows and columns without really affecting anything, so now seemed a good time to put all the rows with exactly one blue cell at the top (having previously established that rows with no blue cell were a disaster for achieving 6m), and all the columns with one blue cell at the left. I said there were 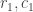$r_1,c_1$ such rows and columns. Then, I put all the columns which had a blue cell in common with the 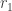$r_1$ rows next to the 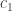$c_1$ columns I already had. Any such column has at least three blues in it, so I said there were 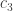$c_3$ of these, and similarly $r_3$ rows. 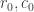The remaining columns and rows might as well be $r_0,c_0$ and hopefully won’t matter too much.

From here, I felt I had all the ingredients, and in fact I did, though some of the book-keeping got a bit fiddly. Knowing what you are aiming for and what you have means there’s only one way to proceed: first expressions in terms of these which are upper bounds for the number of columns (or twice the number of columns = rows if you want to keep symmetry), and lower bounds in terms of these for the number of blue cells. 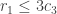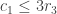I found a noticeable case-distinction depending on whether $r_1\le 3c_3$ and $c_1\le 3r_3$ . If both held or neither held, it was quite straightforward, and if exactly one held, it got messy, probably because I hadn’t set things up optimally. Overall, fiddling about with these expressions occupied slightly more time than actually working out the answer was 6m, so I don’t necessarily have a huge number of lessons to learn, except be more organised.

Afterthought 2: Thought 2 said to consider bipartite graphs. I thought about this later while cycling home, because one can’t (or at least, I can’t) manipulate linear inequalities in my head while negotiating Oxford traffic and potholes. I should have thought about it earlier. The equality case is key. If you add in the edges corresponding to blue cells, you get a series of copies of $K_{1,3}$ , that is, one vertex with three neighbours. Thus you have three edges for every four vertices, and everything’s a tree. This is a massively useful observation for coming up with a very short proof. You just need to show that there can’t be components of size smaller than 4. Also, I bet this is how the problem-setter came up with it…

Local to Global in Point Set Combinatorics

Posted on April 8, 2014 by dominicyeo

I’ve spent the last few days in Cambridge, helping to run the first camp to select the UK team for the International Mathematical Olympiad. We’ve had two 4.5 hour exams, replicating what six of the students will face in the final competition, which this year is held in Cape Town, and also lots of problem-solving sessions, introducing the students to different areas of mathematics relevant to the olympiad. For various reasons, I ended up choosing to discuss combinatorial problems involving points and lines with both sets of students. This is an area which is very popular with problem setters (witness for example Question Two at last year’s IMO in Colombia) but which, because of a lack of any real ‘theory’, is often not treated at these camps.

Anyway, 90 minutes is not a lot of time to solve a large number of problems, so I was interested in the notion of using the time to try to teach the students how to have the right sort of ideas to deal with these. Obviously if there were an easy way to teach people to have good ideas, mathematically or otherwise, life would be a whole lot more straightforward. So, given we can’t do that, the next best thing is to have lots of ideas of any kind, and to get practice at choosing which ones seem best reliably and quickly.

We have two problems to consider that are very similar. I’ll state the first one:

Q1: a strip of width w is the set of all points which lie on or between two parallel lines that are a distance w apart. Let S be a set of n>2 points such that any three can be covered by a strip of width 1. Prove that S can be covered by a strip of width 2.

This sort of thing comes up all the time in olympiad combinatorics and beyond. We have some condition that is local, in the sense that it only affects triples of points, but we want to show that the same condition works for all the points together.

The first step is to be clear about what we are looking for. We are looking for a strip, but we have also been given lots of strips, namely the strips covering each triple of points. So the natural thing to do is to construct the strip we are looking for from the strips we have.

The next observation offered was that we might want to combine two strips of width 1 to get a strip of width 2. This is certainly an idea, but a quick check makes you realise it isn’t a very promising idea. Why? Well unless two strips are parallel, it takes an infinite-width strip to cover their union. Ok, so although that wasn’t useful in itself, it now encourages us to focus on constructing the strip we are looking for from a single one of the strips we are given.

It’s not yet clear exactly how we are going to construct the desired strip from the strip we are given. We should be alive to the possibility that 2 might be a weak bound, and actually $1+\epsilon$ would suffice. Or we might have tried some examples. One thing we might have is a strong example of where a strip of width 2 is necessary, and where we can’t add any points which don’t fit in this strip without breaking the first condition.

Maybe this doesn’t help so much. So perhaps we should think not about how to construct the big strip from the little strip, but instead, how to choose the little strip from the large set we have at our disposal. It is at this stage that I feel it is really important to use all the power at our disposal. In many combinatorics problems we have dealing with a discrete set like [n], where the roles of the labels are interchangeable, and so it can sometimes to be difficult to pick out a particular element. For example, it doesn’t matter for induction whether we take [n-1] then add {n} or start with [2,n] and add {1}. When the construction is geometric, we should use the geometry to make life easier in the construction. For example, if we want to induct, we could add the left-most point in some co-ordinate axes, or some point on the convex hull.

In our particular example, we are still trying to decide which strip to work with. If we consider the triple of points which is in some sense hardest to cover with a strip, this might be a sensible thing to work with. Now we need to decide what it means to be hard to cover a triangle with a strip. We might observe that if the triangle has an altitude of height h, we can certainly cover the triangle with a strip of width h. Further playing around convinces us that the minimum width of a strip required to cover a triangle is given by the shortest altitude. So our intuition that it’s hard to cover a triangle if it is large has been made a bit more concrete. We might also observe that we don’t have much flexibility for a strip if one of the lengths of the triangle is very long. For fixed strip width, as the length of the triangle gets large, the range of angles the strip could sit at (if it is possible at all) gets small.

This motivates considering the least convenient triangle as the one with maximal width and maximal height of altitude. We might try both orders, but certainly considering the triangle ABC such that d(A,B) is maximal among the set of points, and d(AB, C) is maximal once A,B are determined, is useful. The fact that we can cover ABC with one of the strips tells us from the above that $d(AB,C)\le 1$ , and suddenly we are almost done, as we now have a strong clue for what the strip we are looking for should be. If we take all the points x such that $d(AB,x)\le 1$ , we have a strip of width 2, and by construction of C we must have included all points of the set.

The key ingredient here was using what we already had, realising it probably wasn’t going to be helpful to attempt to use *all* of what we already had, then coming up with a sensible way to choose which pre-existing strip to develop.

With this in mind, the next question seems a lot easier:

Q2: Given n points in the plane such that any three lie within some circle of radius 1, prove that *all* the points lie within some circle of radius 1.

Circulating round the room, there were lots of pairs of compasses out and various diagrams of interlocking circles snaking around pieces of A4. But after discussing Q1, suddenly all seems a lot more clear. Similarly to the previous case, we have a lot of circles, and we are looking for a circle. Conveniently, the circle we are looking for is even the same size as the circles we have.

So we need to choose which circle we already have is likely to be most useful. Suppose we have three points very close together. Then we know very little about the circle containing those points – it could be almost anything. By contrast, if we have three points which form a triangle with circumradius equal to 1, then there is in fact no choice about what the covering circle could be. So this is most likely to be useful. So we conjecture that we should consider the triangle with largest circumradius. In fact, this is a problem: if the triangle is obtuse, then the circumradius might actually be greater than 1, but the points still satisfy the condition. In that case, it makes sense to consider the circle with diameter given by the longest side of the triangle.

With that clarification, we now have a collection of circles with radii all $\le 1$ , which cover the triangles. We conjecture that the circle with largest radius might cover all the points. This turns out to be correct, and not too difficult to prove. Both these problems are in some sense extremal. Only here the tricky part was deciding what to extremise. But all were agreed that with some meta-thinking, we were able to decide fairly accurately which ideas were leading towards progress, and following them led fairly rapidly to this extremal property.

Bijections, Prufer Codes and Cayley’s Formula

Posted on April 4, 2013 by dominicyeo

I’m currently at the training camp in Cambridge for this year’s UK IMO squad. This afternoon I gave a talk to some of the less experienced students about combinatorics. My aim was to cover as many useful tricks for calculating the sizes of combinatorial sets as I could in an hour and a half. We started by discussing binomial coefficients, which pleasingly turned out to be revision for the majority. But my next goal was to demonstrate that we are much more interested in the fact that we can calculate these if we want than in the actual expression for their values.

Put another way, my argument was that the interpretation of $\binom{n}{m}$ as the number of ways to choose m objects from a collection of n, or the number of up-and-right paths from (0,0) to (m,n) is more useful than the fact that $\binom{n}{m}=\frac{n!}{m!(n-m)!}$ . The opening gambit was to prove the fundamental result underlying the famous construction of Pascal’s triangle that

$\binom{n+1}{m+1}=\binom{n}{m}+\binom{n}{m+1}.$

This is not a hard result to prove by manipulating factorials, but it is a very easy result to prove in the path-counting setting, for example.

So it turned out that the goal of my session, as further supported by some unsubtly motivated problems from the collection, was to convince the students to use bijections as much as possible. That is, if you have to count something awkward, show that counting the awkward thing is equivalent to counting something more manageable, then count that instead. For many simpler questions, this equivalence is often drawn implicitly using words (“each of the n objects can be in any subset of the collection of bags so we multiply…” etc), but it is always worth having in mind the formal bijective approach. Apart from anything else, asking the question “is this bijection so obvious I don’t need to prove it” is often a good starting-point for assessing whether the argument is in fact correct!

Anyway, I really wanted to show my favouriite bijection argument, but there wasn’t time, and I didn’t want to spoil other lecturers’ thunder by defining a graph and a tree and so forth. The exploration process encoding of trees is a strong contender, but today I want to define quickly the Prufer coding for trees, and use it to prove a famous result I’ve been using a lot recently, Cayley’s formula for the number of spanning trees on the complete graph with n vertices, $n^{n-2}$ .

We are going to count rooted trees instead. Since we can choose any vertex to be the root, there are $n^{n-1}$ rooted trees on n vertices. The description of the Prufer code is relatively simple. Take a rooted tree with vertices labelled by [n]. A leaf is a vertex with degree 1, other than the root. Find the leaf with the largest label. Write down the label of the single vertex to which this leaf is connected, then delete the leaf. Now repeat the procedure, writing down the label of the vertex connected to the leaf now with the largest label, until there are only two vertices remaining, when you delete the non-root vertex, and write down the label of the root. We get a string of (n-1) labels. We want to show that this mapping is a bijection from the set of rooted trees with vertices labelled by [n] to $[n]^{n-1}$ .

Let’s record informally how we would recover a tree from the Prufer code. First, observe that the label of any vertex which is not a leaf must appear in the code. Why? Well, the root label appears right at the end, if not earlier, and every vertex must be deleted. But a vertex cannot be deleted until it has degree one, so the neighbours further from the root (or ancestors) of the vertex must be removed first, and so by construction the label appears. So know what the root is, and what the leaves are straight away.

In fact we can say slightly more than this. The number of times the root label appears is the degree of the root, while the number of times any other label appears is the degree of the corresponding vertex minus one. Call this sequence the Prufer degrees.

So we construct the tree backwards from the leaves towards the root. We add edges one at a time, with the k-th edge joining the vertex with the k-th label to some other vertex. For k=1, this other vertex is the leaf with maximum label. In general, let $G_k$ be the graph formed after the addition of k-1 edges, so $G_1$ is empty, and $G_n$ is the full tree. Define $T_k$ to be the set of vertices such that their degree in $G_k$ is exactly one less than their Prufer degree. Note that $T_1$ is therefore the set of leaves suggested by the Prufer code. So we form $G_{k+1}$ by adding an edge between the vertex with label appearing at position k+1 in the Prufer sequence and the vertex of $T_k$ with maximum label.

Proving that this is indeed the inverse is a bit fiddly, more because of notation than any actual mathematics. You probably want to show injectivity by an extremal argument, taking the closest vertex to the root that is different in two trees with the same Prufer code. I hope it isn’t a complete cop out to swerve around presenting this in full technical detail, as I feel I’ve achieved by main goal of explaining why bijection arguments can reduce a counting problem that was genuinely challenging to an exercise in choosing sensible notation for proving a fairly natural bijection.

Of Triangular Numbers and Bijections (provosta.wordpress.com)
The Canonical Bijective Homomorphism (caltech.typepad.com)
Uniform Spanning Trees (eventuallyalmosteverywhere.wordpress.com)
Linear time labeling algorithm for a tree? (cs.stackexchange.com)

Cambridge Linyi Summer School 2012 – Part Six – Jinan and Home

Posted on August 25, 2012 by dominicyeo

Thursday 23rd August

Whatever conspiracy theories were proposed yesterday were proved unfounded, as today we do indeed go to the mountain. First, however, are the student presentations. I am paired with Jonas, so my students present first to his group, then the reverse. I am extremely pleased with the Markov Chains presentations – it is clear that the speakers have not only understood much of the course than I’d suspected, but have put a great deal of thought and time into preparing a talk that would be well-selected, interesting and intelligible. Given what a disaster would result if I had to give a talk on probability in a foreign language, we were all very impressed with the standard of English shown in all the talks as well. I think everyone is agreed that this was an excellent high point on which to end our trip to Linyi.

Anyway, finally we are off to the Meng Shan mountain. The first stop is a family-run restaurant at the roadside on the edge of the forest park. While we drink tea on stools, we see a chicken being fetched from the outside coop by a Chinese lady with a cleaver and a determined glint in her eye. Sadly, our meal is meat-free, though some of the seasoning and spices go a long way to disproving the assertion that all vegetarian food is bland. The toilet is out back in an ominous brick hut in the middle of the apple orchard. To describe it as a ****hole would be inaccurate. There was no hole. Chris has evidently chosen a bad day for his experience of what our illustrious leader in absentia Marj Batchelor euphemistically defined as V&D. I view this as divine retribution for his shameless attempts to peer pressure me into the club last night.

The mountain itself is a maze of paths through forests, rocks and waterfalls. We are relatively pleased with the cardiovascular exertions of the journey to the main waterfall, until Georgios, who has forsaken the climb for a cable car tour, informs us we saw merely a quarter of the resort. Highlights include the questionable English on pretty much every visible sign, attempting to identify the silhouette of a sleeping Buddha apparently formed by a valley (topology in action?) and the tourist’s t-shirt declaring ‘Love Oneself. Slow. Vicious.’ Glibness aside, the view from the summit was astonishing, and rounded off an excellent visit.

Friday 24th August

Our final morning in Linyi is a ceremonial one. First we each receive a scroll, featuring a quotation by Linyi’s most famous philosopher, as notated by Linyi’s most famous calligrapher. Then we trek across campus for the obligatory photograph next to the stone commemorating the first edition of this summer school, adorned with sage words from Confucius and Dr Marj Batchelor. All that remains is to pack and brace oneself for the four hour drive across Shandong province to the capital, Jinan. Some of the students (who have come from universities in Jinan) are travelling with us. Evidently they had limited faith in the Linyi University accommodation, as we are sharing the bus with twenty duvets…

This is probably an excellent moment to thank the staff at Linyi, in particular Dr Lu, for everything they’ve done to organise and run this summer school. Everyone has been entirely helpful and welcoming, and we’ve all enjoyed our stay a great deal. Also Yuan, my teaching assistant, for her assistance with everything from translating probabilistic notation to advice on ice cream flavours!

I spend some of the journey thinking about whether you can think of measures and metrics as the same thing. I decide that you can’t. More accurately, I decide that I can’t. We are being housed in an impressive hotel on the campus at Shandong Polytechnic. A reunion with hot showers is most welcome. Dinner with our host professors is an astonishing spread. After everyone receives an amuse-bouche of a lightly sauteed sea cucumber, a dazzling array of local dishes arrive. The highlights are oysters, a ferociously spicy brain soup and a trio of donkey meats. We are strongly encouraged to try everything, and though it is a pleasure I am enormously full afterwards, and slightly nervous about maintaining my digestive composure during a 9am research talk tomorrow.

Saturday 25th August

If two attempts at delivering ‘Coalescence: various modern perspectives’ have taught me anything, it’s that I really need to improve my title selection skills. The schedule runs fairly late today, so the four speakers are asked at the last minute to cut the talks to 20 minutes, including time for questions and non-simultaneous translation, which proves a challenge too far. I overrun slightly so as to make sure I have actually got somewhere in terms of content. Many of the audience leave directly after my talk. I can only assume there is an unmissable commitment elsewhere in Jinan at 10.25 rather than any reflection on the quality…

After lunch, we are taken on a tour of Jinan, with stops at the two most famous sites, the Baotu Spring park, and the Daming Lake. As with some of the sights in Beijing, these are very much places of simple beauty and quiet reflection, and so are rather spoilt by the presence of crowds of tourists. A group of locals poke a floating log with umbrellas in an attempt to persuade a shy turtle to emerge from underneath. I can understand its reluctance. Nonetheless, the more peaceful areas were delightful. There is mild panic when we hear by email that the group departing on the late afternoon train are facing five hour delays. Ruadhai, Richard and I are starting to have misgivings about choosing an overnight train to Beijing for the ’experience’. In preparation, I am cautious in observing calls of gan bei, and avoid all dishes with visible chillis. The lack of any signs at Jinan railway station using the Western alphabet is a bit concerning, especially as our train, the illustrious K47, has a different display to all the other departures. After some pained gesticulation we ascertain that it is running half an hour late, so enjoy the additional time with the packs of people sleeping on the concourse. Eventually, just after midnight, the sleeper from Qingdao pulls in, so we join the human tide down to the platform, to see exactly what awaits us in coach 6…

Sunday 26th August

Well that cliffhanger was entirely justified. It turns out that hard seats rather than beds of some kind have been booked for us. Whether this was out of necessity or to enhance the sense of ‘experience’ I do not know. That said, we still feel like emperors in comparison to the scores of travellers who have standing tickets only. I had been worried that my suitcase might be anti-socially unwieldy, but it was as nothing compared to the guy who was travelling with only a 100kg sack of rice for company. Eventually, with everyone safely on board, and luggage stored in a variety of increasingly improvised locations, we steam off into the night. There is initial confusion when it turns out we have arrived at a different station in Beijing to what we had been expecting, but all is forgotten as we find a McDonalds and so by extension, coffee. Richard is suffering somewhat, but Ruadhai and I managed to get a reasonable amount of sleep, so decide to head across town to the airport. After check-in, I come across Ben – or at least, I think it’s Ben, but then all these Westerners look the same… – so we fill the time by talking about stochastic analysis and trying to spend our last handful of Yuan. The flight home is long and uneventful. The modern art instalment next to Gate 37 at Helsinki airport provides brief distraction, but finally back to London. An excellent trip is at an end!

Cambridge Linyi Summer School 2012 – Part Five – Finishing in Linyi

Posted on August 22, 2012 by dominicyeo

Sunday 19th August

Today’s lectures show greater promise, though we have stalled at around the 15 page mark of James Norris’s canonical textbook. I think a change of direction may be called for on Monday, just to avoid getting bogged down in the same calculations every time. The main excitement today was the burst water pipe caused by yesterday evening’s extraordinary thunderstorm. Annoyingly, I didn’t realise this until after I had loaded my laundry into one of the alfresco washing machines, so won’t have any usable clothes until tomorrow at the earliest. Still, worse things happen at sea. I was surprised to realise that I have now been in China for over two weeks. My only real hardship at this point is the limited choice of carbohydrates. Ruadhai agrees – this the probably the longest time an Irishman has gone without a potato since the Famine.

Monday 20th August

The water has returned to an extent. The shower provides only hot, and the washing machine only cold, but now both me and my clothes are clean so my happiness knows no bounds. We cover invariant distributions in the fifth lecture. I am confused why the students choose to ask only today what ‘distribution’ means when it has featured several times in every session so far. Nonetheless, by talking about convergence to equilibrium, I am glad we are approaching a natural finishing point for the course, as there’s nothing worse than a story with a weak ending. Over dinner there are toasts of varying degrees of seriousness with the dean as Siu is leaving tomorrow. The beer of choice is unsubtly called ‘WHEAT’. Afterwards, Karolina does an excellent job of teaching some basic Latin dance steps to an unexpectedly large gathering of the Cambridge group and some students. The plan for teacher-student bonding over the cha cha cha is a huge success. My many left feet are in high demand, but not quite as much as Jonas’s – I think tall blond Germans are something of a rarity in these parts.

Tuesday 21st August

I decide against including too many examples in today’s lecture and instead race through some material so that I can finish early and leave my students some time to prepare for the presentations which they will give on Thursday. The teaching component of this trip has been a challenge. My main difficulty was that I found it very hard to gauge whether the students were understanding what I was doing. In other situations, you can sense what any problems might be from the audience’s real-time reaction, but in China it is clearly a show of disrespect to make any such demonstration. On the other hand, some of the questions they finally realised it was acceptable to ask towards the end of the course, for example about the eigendecomposition of stochastic matrices, showed that the enterprise might have had some positive effect. And in my final lecture, I managed to get through two hours without breaking either a stick of chalk or the blackboard pulley mechanism for the first time… To celebrate the end of the courses, the group is heading out to a karoake bar in town, but my voice and my brain are tired, and I’m mindful of needing to be in full tenor in a few days, so I refrain. Well that’s the excuse I give: mainly I just despise karoake.

Wednesday 22nd August

Another rest day. For a second time, our planned day trip to the Meng Shan mountain and national park is cancelled because of concerns over the potentially dangerous weather, despite both the forecasts and the actuality showing sun and moderate temperatures all day. I feel rather like the little boy in To the Lighthouse, doomed forever to wonder what might have been. Perhaps reflecting the lack of much to do other than foment, various extravagant conspiracy theories are proposed. Instead we play a great deal more table tennis, and I meet my students briefly to help them prepare their presentations. Disappointingly, it seems several have already gone home, but I am confident those who remain will do a good job tomorrow. After dinner, we find a bar beside the Yi river which seems to be the focal point for the few foreigners who live here. Two Americans, Dwayne and Tom, regale us with stories of a year teaching English privately to the city’s swelling middle class. Most of them seem to revolve around implementations of their patented three-step local seduction technique. Apparently white skin and knowing how to say ‘Hello you sexy bitch’, ‘I have food for two at my apartment’ and ‘I don’t understand’ (in response to any attempt at further conversation) in Mandarin, is enough for a sizeable number of the maidens of Linyi. In case you were wondering, they found their current employment advertised on Craigslist. We also meet a young lady who makes a florid but vaguely plausible claim to be the daughter of a local mafia boss then immediately invites us all to a private room she has booked in a nearby club. Despite extreme attempts at coersion, I feel I have already exceeded my surreality limits for the day.

Cambridge Linyi Summer School 2012 – Part Four – Teaching in Linyi

Posted on August 18, 2012 by dominicyeo

Tuesday 14th August

When it rains in this part of the world, you certainly know about it. The skies turned black during breakfast and I was left feeling grateful for my trusty UKMT- issue umbrella. By the end of the day, however, there was no sign of any respite, and the way onto the campus resembled a river more than a road. We were invited to lunch with the Vice-President of the university at a nearby hotel. This proves a truly surreal experience. The selection of dishes is far more eclectic than anything we’ve seen so far. The fried cicadas were surprisingly nice. The sauce made all the difference. The slabs of tofu were less of a success, being more reminiscent of scouring pads than anything edible. The quantities were astonishing. Just when we thought we were making progress, we were each brought a pork tenderloin, served with a single segment of orange. A sequence of toasts was made: for each one the call of ‘gan bei’ demanded that we down our beers. Fortunately the glasses were small, but plans to write lectures and examples sheets in the afternoon had to be rearranged hastily! The Vice-President was very keen for everyone to say something in Chinese, especially the girls present, with mixed success. The few hours spent watching ‘Growing up with Chinese’ finally earned some reward. Tomorrow the raison d’etre of the trip begins, with the first lectures of our courses. I think everyone feels reasonably prepared, but also aware that we have no real idea what we should expect.

Wednesday 15th August

In the end, my first lecture went rather better than I could have expected. I had sat in on Robin’s first session in the morning, on basic statistical theory, and was surprised to chat to the students near the back and learn that some of them were not even science students. I guess their timid responses to relatively straightforward questions were understandable for English majors. My group, however, were all Linyi mathematics students and they seemed to have an excellent grasp of basic probability, so we made reasonably fast progress through the prerequisites, despite the language barrier, and so we should be ready to start the course (mine is on Markov chains) proper tomorrow. In many ways, this summer school is not so much about imparting knowledge of particular new subjects. Rather the focus is instead on promoting a Cambridge style of learning mathematics in Linyi, where the majority of learning seems to be via rote. To that end, today was actually a great success. I think choosing slightly easier material for the first lecture made the students feel more comfortable about answering questions in class and going up to the board to attempt various problems. Hopefully this promising trend will continue through the next five days! Meanwhile, as ever after teaching sessions, I cannot believe how tired I feel. Will be having an early night as soon as I have chosen some problems for tomorrow’s examples sheet.

Thursday 16th August

In the morning I give an examples class, in which we go through some exercises consolidating the material introduced yesterday, and then start another two hours of lectures after lunch. I am confused as to why the audience members are rather different to yesterday, but it seems that flexibility is the order of the day. Anyway, we made it through some of the elementary theory of memoryless random variables and Markov chains, with a view to starting work on ‘real’ examples tomorrow.

In other news, my table tennis skills have improved to the point where I was able to beat one of my students. My chopstick technique has enjoyed a similar transformation. The question of why a proud and technologically advanced nation continues to insist that a pair of glorified needles constitutes the best way to manipulate food is a mystery, but if these are the only route to fullness, you’ve rather got to man up and master them. Rice, fried eggs and chickpeas have provided excellent practice to raise one’s ability to the level required for the twice-daily dessert, banana, pear and tomato fruit salad. Meanwhile, our enthusiasm to spend our Yuan has devastated the campus shop’s supply of ice-creams.

Friday 17th August

My afternoon lecture was rather frustrating. We were talking about n-step transition probabilities, and had worked through the case of the general Markov chain with two states. All subsequent problems could be reduced to this, but it was an impossible task to persuade the students to use the general result which had taken us twenty minutes to develop and which was still sitting on the blackboard, rather than diving into another specific eigenvalue search. The problem is surely cultural. Here, great value is placed on being able to perform difficult computations competently, and this lessens the impact of theory which removes the need for repeated calculation. I’m unsure how to resolve the problem, except by continuing to give examples which are increasingly unyielding to ‘brute force’ methods. Tomorrow is a rest day, so there are plans afoot to examine the nightlife in the city centre with some other foreign residents in our building. I am exhausted by the combination of unrelenting heat and mathematics, so opt instead to join the group watching Groundhog Day in the kitchen. Although my feeling of ennui has declined sharply since the teaching began, aspects of the film feel dangerously similar to two weeks of maths at Linyi University.

Saturday 18th August

We have a day off to mark the halfway point of the teaching week. There is some consternation to learn that the main door to our accommodation, which also serves as the fire exit, is closed with a bike lock overnight. Conversely, our hosts have learned about last night’s club trip, and are apparently ‘very concerned’ for our safety. Hopefully some form of entente will be reached very soon. After lunch a group heads into the city once again, for a taste of ‘real’ life in China. Standards of public hygiene are, well, different. Everyone spits everywhere, and on the bus a mother holds out her little girl to pee all over the floor. Georgios is horrified – such indelicacy would be inconceivable in Athens. Our first stop is an enormous bookshop. Sections are devoted to, amongst others, poultry, adhesive science, and mushroom cultivation. Sadly mathematics does not feature. Jonas is amused to see an aisle devoted to Bildungsroman. This turns out to feature a collection of children’s adventures, all of whose characters appear to be Aryan. I retire to the piano music section. It is clear why the stereotype of prodigious young Chinese pianists exists. The majority of the available repertoire is etudes. That is an unhealthy quantity of Czerny and Burgmuller. I find some Debussy, Schoenberg and the complete Prokofiev sonatas in reasonable editions for a ridiculously low price. The joys of capitalist consumerism

Cambridge Linyi Summer School 2012 – Part Three – Talks in Linyi

Posted on August 13, 2012 by dominicyeo

Friday 10th August

On the Word document controlling the schedule of the summer school, today’s itinerary takes up more room than the rest of the fortnight combined. First up is the official opening ceremony. In the university’s main hall are sixteen armchairs with sixteen steaming pots of green tea set for our group, while the chancellor and the dean make the usual welcoming speeches, before a stream of photographs. After lunch, we are treated to a tour of the campus, and in particular the museum recording the history of the university. The exhibits detailing visits of influential local figures to the building site had an impact that was perhaps slightly lost in translation, but everyone enjoyed the large-scale model of the campus, partly because of its intricacy but also for its assistance in navigating the confusingly sprawling 6km wide site.

An opening banquet is scheduled for the evening, and indeed we turn up at the dining room to find an impressive spread on the lazy Susan. Soups, squids and a whole roasted carp are just the start as the dishes keep on arriving faster than we can possibly make possibly attend to them. We later find out that because the university party chairman could not make the date, this was not in fact the ceremonial dinner. We are intrigued to find out how the banquet could conceivably surpass this?

Saturday 11th August

The mathematical programme begins. For three days there is a series of seminars given by the Cambridge contigent and staff and students from Linyi, all in English. The quality is naturally quite mixed, but I doubt my mathematics would be up to much if I had to deliver a talk in Chinese! There is some confusion about pre-requisite knowledge: Georgios’ talk on ‘Post-Grothendieck Categorical Galois Theory’ gets off to a shaky start when the local students make it clear that they know neither what a category nor a Galois group is. Even the notion of a group causes some murmurings, so he decides to start from the very beginning instead. I don’t mind in the least: now I know the definition of a category! As lunch and dinner come round again, it becomes clear that last night’s feast was no rarity. The campus shop’s selection of red bean paste flavoured ice cream is also a new candidate for my favourite thing ever. My worries about eating well are no longer. For the princely sum of 6 Yuan (about 60p), we find a bottle of the local spirit from the campus supermarket. It smells like over-fermented Malibu but has a surprisingly complicated palate. The initial sensation of peaches gives way to something more woody and finally a heady aftertaste of anti-freeze.

Sunday 12th August

Another full day of seminars. The maths department at Linyi seems to specialise in graph theory, so I get to remind myself of the world of hyper-edges and vertex colouring problems. The highlight of the day is a trip into town. Well, I say town, but in fact Linyi is a city of 10 million people, according to Wikipedia. In spite of that, there doesn’t seem to be a whole lot to do in the centre of town, at least by the standards of Western cities. We have a look at the People’s Square then find a rapid restaurant, where a plate of noodles is a nice change from the rice that is the staple at the university. Afterwards, there are plans to find a bar, but Linyi seems to be somewhat lacking. Instead we check out a supermarket, where the few who remain outside are a major tourist attraction, and the rest of us examine the spirits aisle, where the local brew comes in varieties ranging from 6 to 17,000 Yuan. Unsurprisingly, the student mentality remains and we aim for the lower end of that range. An interesting evening, but with two weeks here remaining, it is slightly worrying that we might already have seen the best of Linyi.

Monday 13th August

I give my research seminar this morning. I choose to talk about coalescence, in particular the multiplicative kernel, essentially describing the skeleton of my Part III essay. It seemed reasonably suitable as it was possible to talk about several ideas and methodologies without actually working through any of the analysis involved in full. It also seemed an excellent opportunity to practise giving a talk on very little preparation. After all, apart from about five Cambridge people, no-one in the audience spoke much English… It was clear from the platform that many of the local undergraduates were engaged in other activities, and most of the remainder just smiled and nodded irrespective of the content. Nonetheless a worthwhile experience. Later, we were able to get into the university’s sports centre. On the ground floor we were greeted by the sight of thirty yellow-shirted ten year olds practising table tennis backhands in regimented unison with astonishing efficiency. The rooms upstairs were a bit less congested, and it was excellent to work off some energy in a way that maths can never quite achieve. And I suspect that by the time we leave, we may all be quite a lot better at badminton!

Cambridge Linyi Summer School 2012 – Part Two – Beijing continued

Posted on August 9, 2012 by dominicyeo

Tuesday 7th August

An early start to beat the Beijing rush hour. I’ve booked myself onto a bus tour of the area north of the city, including a visit to the famous Great Wall. First though, we stop at the Ming dynasty tomb at Dingling. Inside the burial chambers, which are dug deep into a wooded mountainside, the tombs themselves are somewhat less impressive than the stone thrones for the emperor and empresses. It turns out that the entire excavation was ransacked by Red Guards during the Cultural Revolution. The relics from the site were left to spoil, and the skeletons of the emperor and empress were removed and burned. Since then, plans to excavate other, grander tombs have been put on hold.

Then on to Mutianyu, a strategically-located mountain pass 70km north of Beijing. There we eat lunch at a rather touristy restaurant boasting the full range of lazy Susans and sweet and sour pork intestines. I get a chance to meet the rest of the group properly: Roger, Alfredo and Africa from Barcelona and Franz and Barbara, a couple from Basel who have spent the past four weeks in outer Mongolia, and have a fortnight left in China! I ask whether this is a once-in-a-lifetime trip and they look shocked – apparently they do this sort of thing every year.

Anyway, afterwards we board the cable car through the forest canopy and up to the wall. Approaching from below, it is a truly impressive spectacle, stretching for further than the eye can see along the skyline. Any Mongol hordes approaching from the north wouldn’t have stood a chance. The humidity is stifling and even the flatter sections feel like a fair hike. The climb up to the Chinese flag at the end of the main restored section proves a struggle for many, and the hawkers who have somehow raised a fridge up there are getting good business from selling water at 30 Yuan a bottle. The physical reality of the Great Wall is breath-taking, but even more so is the thought of the power of spirit than surrounded its construction. Over hundreds of years, for hundreds of miles and in the most inhospitable of locations, walls like this were built, restored and maintained, all by hand, and they endure to this day. Truly awe-inspiring.

Wednesday 8th August

The temperature hits a high of 35 degrees around lunchtime today, so I decide a slightly quieter day is called for. I head for the picturesque Beihai Park behind the Forbidden City, where a white pagoda rises mole-like from the Jade Island in the middle of the central lake. The water is full of Beijingers on pedalos. I feel equally energetic by the time I get to the top of the island – the marvellous view over the lakes and the sprawling hutong is reward enough for the sweat pouring from my forehead. A group of four Chinese twenty-somethings ask me to join them in posing for a photograph, seemingly in each of the 32 possible configurations, but I am in distinctly no rush, and enjoy the chance to practise my Chinese. I feel it is embarassing that the hotel’s talking mynah bird knows more phrases than I do, but it is improving. Mindful of meeting the Cambridge group tomorrow to travel south to Linyi, I spend the hottest hours of the day resting and doing some preparation work for my lecture course. The Guizhou restaurant I chosen for my final dinner in Beijing turned out to have been closed, so I trusted pot luck, and found a place specialising in the cuisine of Xinjiang in the far northwest. Unexpectedly, the meal is accompanied by intermittent belly-dancers and a optimistically enthusiastic guitarist. The food is somewhat less louche, the house special dapanji is a spicy chicken casserole. It is always easy to exaggerate such things, but my ‘small portion’ genuinely would have fed a party of four and left room to spare. I barely make it past the rim of the bowl before declaring defeat and trudging back heavily laden through Dongzhimen.

Thursday 9th August

I squeeze in a quick trip to the Olympic Park before leaving Beijing. For the first time since arriving it is a brilliantly sunny morning, which is somewhat unfortunate since the park is an entirely exposed concrete esplanade. The Bird’s Nest stadium is very striking though, as you wander through the beams which are somehow both disarranged and artful. Opposite, beside the Water Cube, is the food tent – dumplings and noodles as far as the eye can see! I go for steamed pork versions, before a bizarre dessert that describes itself as fried ice cream.

Then it’s time to join the gang at Beijing Nanzhan. The plan to meet is slightly fraught as the station is absolutely enormous (comparable to the Forbidden City on the overhead map) and is the home to six KFC’s, the agreed rendezvous point. Eventually everyone makes it in time for the high speed train south. It’s refreshing to catch up with the familiar faces at 300 km/h. There are 18 of us, so a bus seating 15 is sent to pick us up from the nearest station for the two hour run into Linyi. Only the driver gets a seatbelt. I’m just glad to get a seat. Not that many places are open in Linyi at 9.30, so we end up with our guides at a corner diner in the centre of town. There is confusion about whether the bowl of warm soy milk that everyone receives is a starter, a soup or a dessert. Matters improve with an onion omelette and further dumplings. The accommodation at the university is exciting. My roommate David and I are surprised to find a water-cooler and a widescreen television, yet there are no cupboards, or any other furnishings. The previous occupants have left us a small gift: a string bag of garlic shoved down the back of the TV stand. We spend a slightly futile twenty minutes attempting to swat mosquitos before turning in.

Cambridge Linyi Summer School 2012 – Part One – Travel and Beijing

Posted on August 6, 2012 by dominicyeo

Saturday 4th August

Painfully early start to Heathrow for the start of this Far Eastern mathematical adventure. In the cause of economy, I’m flying on Finnair with a six hour stop in Helsinki. At this point I should mention how grateful we all are for the generous donation from an anonymous Hong Kong businessman which means this part of the trip has been covered. It turns out to be entirely possible to slip into the town centre for a few hours, rather than stay confined in the clean but rather sterile Finnish airport. The weather is beautiful, with not a cloud in the sky as I stop for freshly grilled salmon on the harbourside then wander round the stylish waterfront shops, the two cathedrals and a sprawling park with a stunning greenhouse complex at its centre. The now scorching conditions do nothing to deter the legions of stallholders attempting to shift arctic fox stoles and reindeer fur throws. I return on the regular airport shuttle bus and head for the gate, albeit two hours early, but unbelievably there is an almost infinite supply of flat sofa-chairs, so I can settle down with Fifty Shades of Grey inconspicuously stored on my Kindle. In many ways, Finland has been an excellent, if brief, preparation for China. Firstly, the language is completely unintelligible. Secondly, I stand out like a black sheep amongst the perfect Nordic specimens, at least until the rest of the passengers turn up for my Asian flight. On the other hand, the price of everything here is absurd. Nothing plausible for lunch comes to less than 10 Euros. I’m informed that might well supply several three-course dinners in Beijing… In any case though, my stay here is short, and I’m on the evening flight East.

Sunday 5th August

I get some sleep leaning against the bulkhead, but am still disastrously tired as I yawn my way through border control at 6am Beijing time. I can’t quite face rush hour right now, so have a snooze in the arrivals lounge before making my way across town. I realise I am being royally ripped off by a taxi driver, who refuses to turn on the meter, but I fail to be demanding enough at the appropriate moment. I think he realises that I realise, and looks suitably sheepish, so I only pay a quarter and he seems happy enough. My room contains a bed, which right now is all I want. After a nap, I catch up on some of the Olympics on Chinese TV while I sort my life out. Evidently I missed the British Gold rush, but unfortunately since none of the remarkable medal haul lay in table tennis or badminton, it’s hard to find any relevant highlights. Later, I head out for a stroll through North-East Beijing. It doesn’t take too long to get used to the humidity and the traffic. I’d been apprehensive about the logistics of crossing the road, when right turns are allowed at all times, but as in Vietnam, it seems that if you just keep going at constant velocity the mopeds will swerve around you. I end up at Gui Jie, the ‘Ghost Street’, and location of hundreds of neon-lit, red-lanterned restaurants facades. Amid the imprenetable character displays, I pick one at random. My phrasebook Chinese and frantic gesticulation on both sides is enough to produce a beer and a serving of the Sichuan speciality, Gongbao chicken, with a worrying mountain of chillis and peppercorns piled in a corner. I proceed with caution.

Monday 6th August

Breakfast is a further adventure. I’ve been a massive fan of the jiaozi dumplings at Dojo in Cambridge for ages, and something similar appears here – a bit odd at 8am. Truly odd, however, are the thousand-year eggs, which are pickled raw in mud (thankfully for only two weeks or so) until the yolk turns a dark green-black and the whole thing carries an aroma of the stable. I’m sure they are an acquired taste. I have not acquired this taste yet. On the other hand, the selection of exotic fruit is excellent, and I always approve of plenty of fish in the morning.

Thus fortified, I descend into the efficient underground realm of the Beijing metro to make my way to Tiananmen Square. It is grey but enormous. Even with thousands of visitors you still feel isolated. I wander round Mao’s Mausoleum, but the queue deters me from paying my respects up close. Instead, across the small moat, and under his famous portrait which gazes down on visitors entering the South Gate of the Forbidden City. The crowd meanders through the collection of gates, hall and palaces that make up the residence of the two dynasties worth of emperors and their extensive entourages. Everywhere there is red and blue, and the copper of the elegant roofs. Some of the most interesting sights are to be found in the less grand arcades and more intimate quarters ranging around the gardens at the back of the complex. In many ways the life of the Emperor doesn’t sound all that fun. From as young as three years old, they had a daily schedule of rituals, sacrifices and administrative meetings, with only the court officials and the intriguing eunuchs who guarded the concubines for company. The best bit in a way was the view from the top of the Coal Hill Park opposite, looking down through the lingering mist (or possibly smog…) at the intricate layers that made up the fascinating enclosed city.

One of the more surprising aspects of today’s sightseeing was how few international tourists there are here. The overwhelming majority of the enthusiastic camera-pointers were Chinese. It felt nice, and a pleasant novelty after the likes of Rome and Istanbul to be with the locals even during the most stereotypical of tourist activities. Dinner tonight was much more of a success. On a terrace by the Houhai lake, a picture menu made life much easier, and I enjoyed my whole roasted duck Sichuan-style, even after the disconcerting moment where I discovered the charred remains of what had once evidently been the head, lurking under a pile of peppercorns.