Tag Archives: random tree

Lecture 6 – Local limits

Posted on by
1

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

By this point of the course, we’ve studied several aspects of the Erdos-Renyi random graph, especially in the sparse setting G(n,\frac{\lambda}{n}). We’ve also taken a lengthy detour to revise Galton-Watson trees, with a particular focus on the case of Poisson offspring distribution.

This is deliberate. Note that a given vertex v of G(n,\frac{\lambda}{n}) has some number of neighbours distributed as \mathrm{Bin}(n-1,\frac{\lambda}{n})\stackrel{d}\approx\mathrm{Po}(\lambda), and the same approximation remains valid as we explore the graph (for example in a breadth-first fashion) either until we have seen a large number of vertices, or unless some ultra-pathological event happens, such as a vertex having degree n/3.

In any case, we are motivated by the notion that the local structure of G(n,\frac{\lambda}{n}) is well-approximated by the Galton-Watson tree with \mathrm{Po}(\lambda) offspring, and in this lecture and the next we try to make this notion precise, and discuss some consequences when we can show that this form of convergence occurs.

Deterministic graphs

Throughout, we will be interested in rooted graphs, since by definition we have to choose a root vertex whose local neighbourhood is to be studied. Usually, we will study a sequence of rooted graphs (G_n,\rho_n), where the vertex set of G_n is [n], or certainly increasing in n (as in the first example).

For some rooted graph (G,\rho), we say such a sequence (G_n,\rho_n) converges to (G,\rho) locally if for all radii r\ge 1, we have B_r^{G_n}(\rho_n)\simeq B_r^G(\rho). In words, the neighbourhood around \rho_n in G_n is the same up to radius r as the neighbourhood around \rho in G, so long as n is large enough (for given r).

This is best illustrated by an example, such as T_n, the binary tree to depth n.

If we take \rho_n to be the usual root, then the trees are nested, and converge locally to the infinite binary tree T_\infty. Slightly less obviously, if we take \rho_n to be one of the leaves, then the trees are still nested (up to labelling – ie in the sense of isomorphisms of rooted trees), and converge locally to the canopy tree, defined by a copy of \mathbb{Z}_{\ge 0} with nearest-neighbour edges, and where each vertex n\ge 1 is connected to the root of a disjoint copy of T_{n-1}, as shown below:

Things get more interesting when the root is chosen randomly, for example, uniformly at random, as this encodes more global information about the graphs G_n. In the case where the G_n are vertex-transitive, then if we only care about rooted graphs up to isomorphism, then it doesn’t matter how we choose the root.

Otherwise, we say that G_n converges in the local weak sense to (G,\rho) if, for all r\ge 1 and for all rooted graphs (H,\rho_H),

\mathbb{P}\left( B^{G_n}_r(\rho_n)\simeq (H,\rho_H) \right) \longrightarrow \mathbb{P}\left( B_r^G(\rho)\simeq H\right),

as n\rightarrow\infty.

Alternatively, one can phrase this as a result about convergence of rooted-graph-valued distributions.

A simple non-transitive example is G_n\simeq P_n, the path of length n. Then, the r-neighbourhood of a vertex is isomorphic to P_{2r}, unless that vertex is within graph-distance (r-1) of one of the leaves of G_n. As n\rightarrow\infty, the proportion of such vertices vanishes, and so, \mathbb{P}\left( B^{P_n}_r(\rho_n)\simeq P_{2r}\right)\rightarrow 1, from which we conclude the unsurprising result that P_{n} converges in the local weak sense to \mathbb{Z}. (Which is vertex-transitive, so it doesn’t matter where we select the root.)

The binary trees offer a slightly richer perspective. Let \mathcal{L}_n be the set of leaves of T_n, and we claim that when \rho_n is chosen uniformly from the vertices of T_n, then d_{T_n}(\rho_n,\mathcal{L}_n) converges in distribution. Indeed, \mathbb{P}\left( d_{T_n}(\rho_n,\mathcal{L}_n)=k\right) = \frac{2^{n-k}}{2^{n+1}-1}, whenever n\ge k, and so the given distance converges in distribution to the Geometric distribution with parameter 1/2 supported on {0,1,2,…}.

This induces a random local weak limit, namely the canopy tree, rooted at one of the vertices we denoted by \mathbb{Z}_{\ge 0}, with the choice of this vertex given by Geometric(1/2). Continue reading →

Generating uniform trees

Posted on by
Reply

A long time ago, I wrote quite a few a things about uniform trees. That is, a uniform choice from the n^{n-2} unrooted trees with vertex set [n]. This enumeration, normally called Cayley’s formula, has several elegant arguments, including the classical Prufer bijection. But making a uniform choice from a large set is awkward, and so we seek more probabilistic methods to sample such a tree, which might also give insight into the structure of a ‘typical’ uniform tree.

In another historic post, I talked about the Aldous-Broder algorithm. Here’s a quick summary. We run a random walk on the complete graph 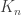K_n started from a uniformly-chosen vertex. Every time we arrive at a vertex we haven’t visited before, we record the edge just traversed. Eventually we have visited all n vertices, so have recorded n-1 edges. It’s easy enough to convince yourself that these n-1 edges form a tree (how could there be a cycle?) and a bit more complicated to decide that the distribution of this tree is uniform.

It’s worth noting that this algorithm works to construct a uniform spanning tree on any connected base graph.

This post is about a few alternative constructions and interpretations of the uniform random tree. The first construction uses a Galton-Watson process. We take a Galton-Watson process where the offspring distribution is Poisson(1), and condition that the total population size is n. The resulting random tree has a root but no labels, however if we assign labels in [n] uniformly at random, the resulting rooted tree has the uniform distribution among rooted trees on [n].

Proof

This is all about moving from ordered trees to non-ordered trees. That is, when setting up a Galton-Watson tree, we distinguish between the following two trees, drawn extremely roughly in Paint:

That is, it matters which of the first-generation vertices have three children. Anyway, for such a (rooted) ordered tree T with n vertices, the probability that the Galton-Watson process ends up equal to T is

\mathbb{P}(GW = T) = \prod_{v\in T} \frac{e^{-1}}{C(v)!} = e^{-n} \prod_{v\in T}\frac{1}{C(v)!},

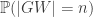where C(v) is the number of children of a vertex v\in T. Then, since \mathbb{P}( |GW|=n ) is a function of n, we find

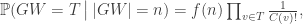
\mathbb{P}(GW=T \,\big|\, |GW|=n) = f(n)\prod_{v\in T} \frac{1}{C(v)!},

where f(n) is a function of n alone (ie depends on T only through its size n).

But given an unordered rooted tree t, labelled by [n], there are \prod_{v \in t} C(v)! ordered trees associated to t in the natural way. Furthermore, if we take the Poisson Galton-Watson tree conditioned to have total population size n, and label uniformly at random with [n], we obtain any one of these ordered trees with probability \frac{f(n)}{n!} \prod_{v\in t} \frac{1}{C(v)!}. So the probability that we have t after we forget about the ordering is \frac{f(n)}{n!}, which is a function of n alone, and so the distribution is uniform among the set of rooted unordered trees labelled by [n], exactly as required.

Heuristic for Poisson offspring distribution

In this proof, the fact that 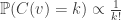\mathbb{P}(C(v)=k)\propto \frac{1}{k!} exactly balances the number of orderings of the k children explains why Poisson(1) works out. Indeed, you can see in the proof that Poisson(c) works equally well, though when c\ne 1, the event we are conditioning on (namely that the total population size is n) has probability decaying exponentially in n, whereas for c=1, the branching process is critical, and the probability decays polynomially.

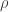We can provide independent motivation though, from the Aldous-Broder construction. Both the conditioned Galton-Watson construction and the A-B algorithm supply the tree with a root, so we’ll keep that, and look at the distribution of the degree of the root as constructed by A-B. Let \rho=v_1,v_2,v_3,\ldots be the vertices [n], ordered by their discovery during the construction. Then \rho is definitely connected by an edge to 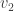v_2, but thereafter it follows by an elementary check that the probability 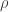\rho is connected to 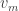v_m is \frac{1}{n-1}, independently across all m. 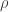In other words, the distribution of the degree of \rho in the tree as constructed by A-B is

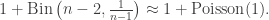
1+ \mathrm{Bin}\left(n-2,\frac{1}{n-1}\right) \approx 1+\mathrm{Poisson}(1).

Now, in the Galton-Watson process, conditioning the tree to have fixed, large size changes the offspring distribution of the root. Conveniently though, in a limiting sense it’s the same change as conditioning the tree to have size at least n. Since these events are monotone in n, it’s possible to take a limit of the conditioning events, and interpret the result as the Galton-Watson tree conditioned to survive. It’s a beautiful result that this interpretation can be formalised as a local limit. The limiting spine decomposition consists of an infinite spine, where the offspring distribution is a size-biased version of the original offspring distribution (and so in particular, always has at least one child) and where non-spine vertices have the original distribution.

In particular, the number of the offspring of the root is size-biased, and it is well-known and not hard to check that size-biasing Poisson(c) gives 1+Poisson(c) ! So in fact we have, in an appropriate limiting sense in both objects, a match between the degree distribution of the root in the uniform tree, and in the conditioned Galton-Watson tree.

This isn’t supposed to justify why a conditioned Galton-Watson tree is relevant a priori (especially the unconditional independence of degrees), but it does explain why Poisson offspring distributions are relevant.

Construction via G(N,p) and the random cluster model

The main reason uniform trees were important to my thesis was their appearance in the Erdos-Renyi random graph G(N,p). The probability that vertices {1, …, n} form a tree component in G(N,p) with some particular structure is

p^{n-1} (1-p)^{\binom{n}{2}-(n-1)} \times (1-p)^{n(N-m)}.

Here, the first two terms give the probability that the graph structure on {1, …, n} is correct, and the the final term gives the probability of the (independent) event that these vertices are not connected to anything else in the graph. In particular, this has no dependence on the tree structure chosen on [n] (for example, whether it should be a path or a star – both examples of trees). So the conditional distribution is uniform among all trees.

If we work in some limiting regime, where pn\rightarrow 0 (for example if n is fixed and p=\frac{1}{N}\rightarrow 0), then we can get away asymptotically with less strong conditioning. Suppose we condition instead just that [n] form a component. Now, there are more ways to form a connected graph with one cycle on [n] than there are trees on [n], but the former all require an extra edge, and so the probability that a given one such tree-with-extra-edge appears as the restriction to [n] in G(N,p) is asymptotically negligible compared to the probability that the restriction to [n] of G(N,p) is a tree. Naturally, the local limit of components in G(N,c/N) is a Poisson(c) Galton-Watson branching process, and so this is all consistent with the original construction.

One slightly unsatisfying aspect to this construction is that we have to embed the tree of size [n] within a much larger graph on [N] to see uniform trees. We can’t choose a scaling p=p(n) such that G(n,p) itself concentrates on trees. To guarantee connectivity with high probability, we need to take p> \frac{\log n}{n}, but by this threshold, the graph has (many) cycles with high probability.

At this PIMS summer school in Vancouver, one of the courses is focusing on lattice spin models, including the random cluster model, which we now briefly define. We start with some underlying graph G. From a physical motivation, we might take G to be 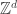\mathbb{Z}^d or some finite subset of it, or a d-ary tree, or the complete graph 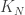K_N. As in classical bond percolation (note G(N,p) is bond percolation on 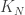K_N), a random subset of the edges of G are included, or declared open. The probability of a given configuration w, with e open edges is proportional to

p^e (1-p)^{|E(G)| - e} q^{k(w)}, (*)

where the edge-weight 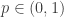p\in(0,1) as usual, and cluster weight q\in (0,\infty), and k(w) counts the number of connected components in configuration w. When q=1, we recover classical bond percolation (including G(N,p) ), while for q>1, this cluster-reweighting favours having more components, and q<1 favours fewer components. Note that in the case q\ne 1, the normalising constant (or partition function) of (*) is generally intractable to calculate explicitly.

As in the Erdos-Renyi graph, consider fixing the underlying graph G, and taking 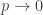p\rightarrow 0, but also taking \frac{q}{p}\rightarrow 0. So the resulting graph asymptotically ‘wants to have as few edges as possible, but really wants to have as few components as possible’. In particular, 1) all spanning trees of G are equally likely; 2) any configuration with more than one component has asymptotically negligible probability relative to any tree; 3) any graph with a cycle has #components + #edges greater than that of a tree, and so is asymptotically negligible probability relative to any tree.

In other words, the limit of the distribution is the uniform spanning tree of G, and so this (like Aldous-Broder) is a substantial generalisation, which constructs the uniform random tree in the special case where G=K_n.

 

The Rearrangement Inequality

Posted on by
1

A favourite result of many students doing olympiad inequality problems is the so-called Rearrangement Inequality. This is a mathematical formulation of the idea well-known to even the smallest of child that if you prefer cakes to carrots then if you are offered two of one and one of the other, you should take two of the one you prefer!

At a more formal level, it says that given two strings of non-negative numbers

a_1\le a_2,\le \ldots\le a_n, \quad b_1\le b_2\le \ldots\le b_n,

if you want to form a sum of products of pairs, like

a_1b_4+a_2b_1+a_3b_3+\ldots,

you get the largest result if you take

a_1b_1+a_2b_2+\ldots+a_nb_n.

Formally, for any permutation \sigma \in S_n,

a_1b_1+\ldots+a_nb_n\ge a_1b_{\sigma(1)}+\ldots+a_nb_{\sigma(n)}\ge a_1b_n+\ldots+a_nb_1.

That is, you multiply the largest terms in each sequence together.

The notation to describe to equality case is a bit annoying. Essentially, the sums are equal if and only if the summands exactly correspond. If the sequences are strictly increasing, then equality holds only if the permutation \sigma=\text{id}.

This result is nice because, although it is rarely explicitly useful, it goes in a different direction from the standard scheme of results strengthening AM-GM, Cauchy-Schwarz and so on, and is in some sense more intuitive than these more well-known inequalities, at least in the form presented in an olympiad context.

I was thinking about this partly because it’s a nice result in its own right, but also because it came up in a research problem to do with comparing the expected likelihood of different tree isomorphism classes arising in an inhomogeneous, but relatively well-behaved, random graph model. The probability of forming a given tree is a homogeneous multivariate polynomial in the ages of the vertices that would form the tree. It is then necessary to integrate over the joint distribution (which fortunately is a product in the limit) of the ages of the vertices. I was playing around with this by considering what seemed to be the extreme cases: the star and the path. I was working with the relatively simple case n=4, and it struck me that perhaps the polynomial for the star was always at least as large as that for the path. This would be convenient as it would avoid the need for a horrific-looking integral calculation. This turned out to be true. My first method was a heavy but uncontroversial convexity and stationary point argument, but I found a pair of vectors embedded in the desired inequality on which I could deploy rearrangement.

Anyway, I thought I should be able to come up with a nice proof, and I think this is one. I think this is particularly nice because it is a demonstration that one can do a proof by induction without explicitly inducting on the natural numbers.

We begin with a base case, which is the theorem for n=2, even though we will not be doing induction in the canonical way. We are required to prove that given

a_1\le a_2,\quad b_1\le b_2,

that

a_1b_1+a_2b_2\ge a_1b_2+a_2b_1,

since these are the only available permutations. Moving some terms around gives

(a_2-a_1)(b_2-b_1)\ge 0,

which is true by construction, and so the n=2 result follows.

We now move straight to the general n case. We focus on the left of the two inequalities in the statement of the result, since the other will follow by an identical method, applied in reverse. We consider the case where \sigma is a transposition. For example, we might consider 12435. When we write out the result we want:

a_1b_1+a_2b_2+a_3b_3+a_4b_4+a_5b_5\ge a_1b_1+a_2b_2+a_3b_4+a_4b_3+a_5b_5,

we realise that many of the terms cancel, and the content of the theorem reduces to the n=2 case we have already dealt with. Obviously, this holds equally well whenever \sigma is a transposition. Similarly, if \sigma is a product of two disjoint transpositions, which means that two disjoint pairs of elements are interchanged, we can apply the n=2 case twice, then add on the extra terms to get the result.

In fact, we can do much better than this, by using the fact that any permutation can be expressed as a product of transpositions. We need to be careful about the risk of asserting that every time we multiply the permutation \sigma by a transposition, the value of the associated sum-product expression gets smaller. While the idea is correct, this cannot be generally true. After all, applying the same transposition twice returns us to the identity permutation!

We can nonetheless say something useful. If we start with a permutation

\sigma(1),\sigma(2),\ldots,\sigma(n),

and we interchange the ith and jth elements, to get,

\tau=\sigma(1),\ldots,\sigma(i-1),\sigma(j),\sigma(i+1),\ldots,\sigma(j-1),\sigma(i),\sigma(j+1),\ldots,\sigma(n),

then the product sum corresponding to \tau is less than or equal to the product sum corresponding to \sigma if $\sigma(i)\leq sigma(j)$, under the implicit assumption that i<j. In other words, we can prove the rearrangement inequality for any permutation \sigma that can be obtained from the identity by repeatedly interchanging elements that are initially in increasing order. Essentially, we have defined a partial ordering on the set of permutations.

It suffices to check that all permutations have this property. In fact, this is relatively easy. We can move element n to its required position in \sigma by successively swapping with (n-1), (n-2), etc. If we set this up as an inductive argument, we can finish by applying the hypothesis to the remaining (n-1) elements, which are in the same order as the identity permutation on [n-1].

So we have proved the left-hand side of the Rearrangement Inequality. In fact, this partial ordering framework makes it clear how to prove the right-hand side. By an identical argument, we can get from any permutation to the reverse identity by a similar set of operations.

Related articles

The Contour Process

Posted on by
2

As I explained in my previous post, I haven’t been reading around as much as I would generally like to recently. A few days in London staying with my parents and catching up with some friends has therefore been a good chance to get back into the habit of leafing through papers and Pitman’s book among other things.

This morning’s post should be a relatively short one. I’m going to define the contour process, a function of a (random or deterministic) tree, related to the exploration process which I have mentioned a few times previously. I will then use this to prove a simple but cute result equating in distribution the sizes of two different branching processes via a direct bijection.

The Contour Process

To start with, we have to have a root, and from that root we label the tree with a depth-first labelling. An example of this is given below. It is helpful at this stage to conceive this process as an explorer walking on the tree, and turning back on themselves only when there is no option to visit a vertex they haven’t already seen. So in the example tree shown, the depth-first exploration visits vertex V_2 exactly four times. Note that with this description, it is clear that the exploration traverses every edge exactly twice, and so the length of the sequence is 2n-1, where n is the number of vertices in the tree since obviously, we start and end at the root.

Another common interpretation of this depth-first exploration is to take some planar realisation of the tree. (Note trees are always planar – proof via induction after removing a leaf.) Then if you treat the tree as a hedge and starting at the root walk along, following the outer boundary with your right hand, this exactly recreates the process.

The height of a tree at a particular vertex is simply the graph distance between that vertex and the root. So when we move from one vertex to an adjacent vertex, the height must increase or decrease by 1.

The contour process is the sequence of heights seen along the depth-first exploration. It is therefore a sequence:

0=h_0,h_1,\ldots,h_{2n-1}=0,\quad h_i\geq 0,

and such that |h_{i+1}-h_i|=1.

Note that though the contour process uniquely determines the tree structure, the choice of depth-first labelling is a priori non-canonical. For example, in the display above, V_3 might have been explored before V_2. Normally this is resolved by taking the suitable vertex with the smallest label in the original tree to be next. It makes little difference to any analysis to choose the ordering of descendents of some vertex in a depth-first labelling randomly. Note that this explains why it is rather hard to recover Cayley’s theorem about the number of rooted trees on n vertices from this characterisation. Although the number of suitable contour functions is possible to calculate, we would require a complicated multiplicative correction for labelling if we wanted to recover the number of trees.

The only real observation about the uses of the contour process at this stage is that it is not in general a random walk with IID increments for a Galton-Watson branching process. This equivalence is what made the exploration process so useful. In particular, it made it straightforward, at least heuristically, to see why large trees might have a limit interpretation through Brownian excursions. If for example, the offspring distribution is bounded above, say by M, then the contour process certainly cannot be a random walk, as if we have visited a particular vertex exactly M+1 times, then it cannot have another descendent, and so we must return closer to the root at the next step.

I want to mention that in fact Aldous showed his results on scaling limits towards the Continuum Random Tree through the contour process rather than the exploration process. However, I don’t want to say any more about that right now.

A Neat Equivalence

What I do want to talk about is the following distribution on the positive integers. This comes up in Balazs Rath and Balint Toth’s work on forest-fires on the complete graph that I have been reading about recently. The role of this distribution is a conjectured equilibrium distribution for component size in a version of the Erdos-Renyi process where components are deleted (or ‘struck by lightning’) at a rate tuned so that giant components ‘just’ never emerge.

This distribution has the possibly useful property that it is the distribution of the total population size in a Galton-Watson process with Geom(1/2) offspring distribution. It is also the distribution of the total number of leaves in a critical binary branching process, where every vertex has either two descendents or zero descendents, each with probability 1/2. Note that both of these tree processes are critical, as the expected number of offspring is 1 in each case. This is a good start, as it suggests that the relevant equilibrium distribution should also have the power-law tail that is found in these critical branching processes. This would confirm that the forest-fire model exhibits self-organised criticality.

Anyway, as a sanity check, I tried to find a reason why, ignoring the forest-fires for now, these two distributions should be the same. One can argue using generating functions, but there is also the following nice bijective argument.

We focus first on the critical Geometric branching process. We examine its contour function. As explained above, the contour process is not in general a random walk with IID increments. However, for this particular case, it is. The geometric distribution should be viewed as the family of discrete memoryless distributions.

This is useful for the contour process. Note that if we are at vertex V for the (m+1)th time, that is we have already explored m of the edges out of V, then the probability that there is at least one further edge is 1/2, independently of the history of the exploration, as the offspring distribution is Geometric(1/2), which we can easily think of as adding edges one at a time based on independent fair coin tosses until we see a tail for example. The contour process for this random tree is therefore a simple symmetric random walk on Z. Note that this will hit -1 at some point, and the associated contour process is the RW up to the final time it hits 0 before hitting -1. We can check that this obeys the clear rule that with probability 1/2 the tree is a single vertex.

Now we consider the other model, the Galton-Watson process with critical binary branching mechanism. We should consider the exploration process. Recall that the increments in this process are given by the offspring distribution minus one. So this random sequence also behaves as a simple symmetric random walk on Z, again stopped when we hit -1.

To complete the bijective argument, we have to relate leaves in the binary process to vertices in the geometric one. A vertex is a leaf if it has no offspring, so the number of leaves is the number of times before the hitting time of -1 that the exploration process decreases by 1. (*)

Similarly for the contour process. Note that there is bijection between the set of vertices that aren’t the root and the set of edges. The contour process explores every edge exactly twice, once giving an increase of 1 and once giving a decrease of 1. So there is a bijection between the times that the contour process decreases by 1 and the non-root vertices. But the contour process was defined only up to the time we return to the root. This is fine if we know in advance how large the tree is, but we don’t know which return to the root is the final return to the root. So if we extend the random walk to the first time it hits -1, the portion up until the last increment is the contour process, and the final increment must be a decrease by 1, hence there is a bijection between the number of vertices in the Geom(1/2) G-W tree and the number of times that the contour process decreases by 1 before the hitting time of -1. Comparing with (*) gives the result.

Related articles

Bell Polynomials

Posted on by
4

Trees with a single cycle

When counting combinatorial objects, it is often the case that we have two types of structure present at different levels. The aim of this post is to introduce the Bell polynomials, which provides the most natural notation for describing this sort of situation, and to mention some of the results that become easier to derive in this framework. This post is based on material and exercises from Chapter 1 of Jim Pitman’s book Combinatorial Stochastic Processes, which is great, and also available online here.

The structures that Bell polynomials enumerate are called composite structures in this account. Rather than give a definition right away, I shall give an example. An object I have been thinking about in the past few weeks are graphs on n vertices containing precisely one cycle. Some of the background for this has been explained in recent posts.

In a recent post on Prufer codes, I gave the classical argument showing that the number of trees on n vertices is n^{n-2}. We might consider a unicyclic graph to be a tree with an extra edge. But if we consider the number of ways to add a further vertex to a tree, we get

n^{n-2}\left[\binom{n}{2}-(n-1)\right]=n^{n-2}\binom{n-1}{2}.

Obviously, we have overcounted. If the single cycle in a graph has length k, then the graph has been counted exactly k times in this enumeration. But it is not obvious how many graphs have a single cycle of length k.

Instead, we stop worrying about exactly how many of these there are, as there might not be a simple expression anyway. As soon as we start using them in any actual argument, it will be useful to know various properties about the graphs, but probably not exactly how many there are.

Let’s focus on this single cycle of length k say. If we remove the edges of the cycle, we are left with a collection of trees. Why? Well if there was a cycle in the remaining graph, then the original graph would have had at least two cycles. So we have a collection of trees, unsurprisingly called a forest. Remembering that some of the trees may in fact be a single vertex (on the cycle), it is clear that there is a bijection between these trees and the vertices of the cycle in the obvious way. We can think of the graph as a k-cycle, dressed with trees.

Alternatively, once we have specified its size, we can forget about the k-cycle altogether. The graph is precisely defined by a forest of k trees on n vertices, with a specified root in each tree indicating which vertex lies on the cycle, and a permutation specifying the cyclic ordering of the trees. We can write this as

N_{n,k}=(k-1)!\sum_{(A_1,\ldots,A_k)\in\mathcal{P}^k(n)}a_1^{a_1-1}\cdot\ldots\cdot a_k^{a_k-1},\quad \text{for }a_i=|A_i|,

where \mathcal{P}^k(n) is the number of partitions of [n] with k blocks. Remember that the blocks in a partition are necessarily unordered. This makes sense in this setting as the cyclic permutation chosen from the (k-1)! possibilities specifies the order on the cycle.

Bell Polynomials

The key point about this description is that there are two types of combinatorial structure present. We have the rooted trees, and also a cyclic ordering of the rooted trees. Bell polynomials generalise this idea. It is helpful to be less specific and think of partitions of [n] into blocks. There are w_j arrangements of any block of size j, and there are v_k ways to arrange the blocks, if there are k of them. Note that we assume v_k is independent of the arrangements within the collection of blocks. So in the previous example, w_j=j^{j-2}, and v_k=(k-1)!. Pitman denotes these sequences by v_\bullet,w_\bullet. Then the (n,k)th partial Bell polynomial, B_{n,k}(w_\bullet) gives the number of divisions into k blocks:

B_{n,k}(w_\bullet):=\sum_{(A_1,\ldots,A_k)\in\mathcal{P}^k(n)}\prod_{i=1}^k w_{a_i}.

The total number of arrangements is given by the Bell polynomial

B_n(v_\bullet,w_\bullet):=\sum_{k=1}^n v_k B_{n,k}(w_\bullet).

Here are some other examples of Bell polynomials. The Stirling numbers of the first kind c_{n,k} give the number of permutations of [n] with k cycles. Since we don’t want to impose any combinatorial structure on the set of cycles, we don’t need to consider v_\bullet, and the number of ways to make a j-cycle from a j-block is w_j=(j-1)!, so c_{n,k}:=B_{n,k}((\bullet-1)!). Similarly, the Stirling numbers of the second kind S_{n,k} give the number of permutations of [n] into k blocks. Almost by definition, S_{n,k}:=B_{n,k}(1^\bullet), where $1^\bullet$ is defined to be the sequence containing all 1s.

Applications

So far, this is just a definition that gives an abbreviated description for the sizes of several interesting sets of discrete objects. Having clean notation is always important, but there are further advantages of using Bell polynomials. I don’t want to reproduce the entirety of the chapter I’ve read, so my aim for this final section is to give a very vague outline of why this is a useful formulation.

Bell polynomials can be treated rather nicely via generating functions. The key to this is to take a sum not over partitions, but rather over ordered partitions, which are exactly the same, except now we also care about the order of the blocks. This has the advantage that there is a correspondence between ordered partitions with k blocks and compositions with k terms. If the composition is n_1+\ldots+n_k=n, it is clear why there are \binom{n}{n_1,\ldots,n_k} ordered partitions encoding this structure. This multinomial coefficient can be written as a product of factorials of $n_i$s over i, and so we can write:

B_{n,k}(w_\bullet)=\frac{n!}{k!}\sum_{(n_1,\ldots,n_k)}\prod_{i=1}^k \frac{w_{n_i}}{n_i!}.

This motivates considering the exponential generating function given by

w(\xi)=\sum_{j=1}^\infty w_j\frac{\xi_j}{j!},

as this leads to the neat expressions:

B_{n,k}(w_\bullet)=n![\xi^n]\frac{w(\xi)^k}{k!},\quad B_n(v_\bullet,w_\bullet)=n![\xi^n]v(w(\xi)).

The Bell polynomial B_n(v_\bullet,w_\bullet) counts the number of partitions of [n] subject to some extra structure. If we choose uniformly from this set, we get a distribution on this combinatorial object, for which the Bell polynomial provides the normalising constant. If we then ignore the extra structure, the sequences v_\bullet,w_\bullet induce a probability distribution on the set of partitions of n. This distribution is known as a Gibbs partition. It is interesting to consider when and whether it is possible to define a splitting mechanism such that the Gibbs partitions can be coupled to form a fragmentation process. This is the opposite of a coalescence process. Here, we have a sequence of masses, and at each integer time we have rules to determine which mass to pick, and a rule for how to break it into two pieces. It is certainly not the case that for an arbitrary splitting rule and sequences v_\bullet,w_\bullet, the one-step fragmentation of the Gibbs partition on n gives the corresponding Gibbs partition on (n-1).

CLT for random permutations

For the final demonstration of the use of Bell polynomials, I am going to sketch the outline of a solution to exercise 1.5.4. which shows that the number of cycles in a uniformly chosen permutation has a CLT. This is not at all obvious, since the number of permutations of [n] with k cycles is given by B_{n,k}((\bullet-1)!) and there is certainly no simple form for this, so the possibility of doing a technical limiting argument seems slim.

For ease of notation, we copy Pitman and write c_{n,k}:=B_{n,k}((\bullet-1)!) as before. First we show exercise 1.2.3. which asserts that

x(x+1)\ldots(x+(n-1))=\sum_{k=1}^n c_{n,k}x^k.

We argue combinatorially. The RHS is the number of ways to choose \sigma\in S_n and a colouring of [n] with k colours such that the orbits of \sigma are monochromatic. We prove that the LHS also has this property by induction on the number of vertices. We claim there is a 1-to-(x+n) map from configurations on n vertices to configurations on (n+1) vertices. Given \sigma\in S_n and colouring, for any a\in[n], we construct \sigma_a\in S_{n+1} by \sigma_a(a)=n+1, \sigma_a(n)=\sigma(a) and for all other x, \sigma_a(x)=\sigma(x). We give n+1 the same colour as a. This gives us n possibilities. Alternatively, we can map (n+1) to itself and give it any colour we want. This gives us x possibilities. A slightly more careful argument shows that this is indeed a 1-to-(x+n) map, which is exactly what we require.

So the polynomial

A_n(z)=\sum_{k=0}^nc_{n,k}z^k,

has n real zeros, which allows us to write

\frac{c_{n,k}}{A_n(1)}=\mathbb{P}(X_1+\ldots+X_n=k),

where the Xs are independent but not identically distributed Bernoulli trials. The number of cycles is then given by this sum, and so becomes a simple matter to verify the CLT by checking a that the variances grows appropriately. As both mean and variance are asymptotically log n, we can conclude that:

\frac{K_n - \log n}{\sqrt{\log n}}\stackrel{d}{\rightarrow} N(0,1).

In a future post, I want to give a quick outline of section 1.3. which details how the Bell polynomials can be surprisingly useful to find the moments of infinitely divisible distributions.

Related articles

Diameters of Trees and Cycle Deletion

Posted on by
1

In the past two posts, we introduced two models of random trees. The Uniform Spanning Tree chooses uniformly at random from the set of spanning trees for a given underlying graph. The Minimum Spanning Tree assigns IID weights to each edge in the underlying graph, then chooses the spanning tree with minimum induced total weight. We are interested to know whether these are in fact the same distribution, and if they are not, what properties can be used to distinguish them asymptotically.

While investigating my current research problem, I was interested in the diameter of large random trees under various models. Specifically, I am considering what happens if you take a standard Erdos-Renyi process on n vertices, where edges appear at constant rate between pairs of vertices chosen uniformly at random, and add an extra mechanism to prevent the components becoming too large. For this particular model, our mechanism consists of removing any cycles as they are formed. Thus all the components remain trees as time advances, so it is not unreasonable to think that there might be some sort of equilibrium distribution.

Now, by definition, any tree formed by the Erdos-Renyi process is a uniform tree. Why? Well, the probability of a configuration is determined entirely by the number of edges present, so once we condition that a particular set of vertices are the support of a tree, all possible tree structures are equally likely. Note that this relies on sampling at a single fixed time. If we know the full history of the process, then it is no longer uniform. For example, define a k-star to be a tree on k vertices where one ‘centre’ vertex has degree k-1. The probability that a uniform tree on k vertices is a k-star is \frac{k}{k^{k-2}}=k^{-(k-3)}. But a star can only be formed by successively adding single vertices to an existing star. That is, we cannot join a 3-tree and a 4-tree with a edge to get a 7-star. So it is certainly not immediately clear that once we’ve incorporated the cycle deletion mechanism, the resulting trees will be uniform once we condition on their size.

In fact, the process of component sizes is not itself Markovian. For a concrete example, observe first that there is, up to isomorphism, only one tree on any of {0,1,2,3} vertices, so the first possible counterexample will be splitting up a tree on four vertices. Note that cycle deletion always removes at least three edges (ie a triangle), so the two possibilities for breaking a 4-tree are:

(4) -> (2,1,1) and (4) -> (1,1,1,1)

I claim that the probabilities of each of these are different in the two cases: a) (4) is formed from (2,2) and b) (4) is formed from (3,1). This is precisely a counterexample to the Markov property.

In the case where (4) is formed from (2,2), the 4-tree is certainly a path of length 4. Therefore, with probability 1/3, the next edge added creates a 4-cycle, which is deleted to leave components (1,1,1,1). In the case where (4) is formed from (3,1), then with probability 2/3 it is a path of length 4 and with probability 1/3 it is a 4-star (a ‘T’ shape). In this second case, no edge can be added to make a 4-cycle, so after cycle deletion the only possibility is (2,1,1). Thus the probability of getting (1,1,1,1) is 2/9 in this case, confirming that the process is non-Markovian. However, we might remark that we are unlikely to have O(n) vertices involved in fragmentations until at least the formation of the giant component in the underlying E-R process, so it is possible that the cycle deletion process is ‘almost Markov’ for any property we might actually be interested in.

When we delete a cycle, how many vertices do we lose? Well, for a large tree on n vertices, the edge added which creates the cycle is chosen uniformly at random from the pairs of vertices which are not currently joined by an edge. Assuming that n is w(1), that is we are thinking about a limit of fairly large trees, then the number of edges present is much smaller than the number of possible edges. So we might as well assume we are choosing uniformly from the possible edges, rather than just the possible edges which aren’t already present.

If we choose to add an edge between vertices x and y in the tree, then a cycle is formed and immediately deleted. So the number of edges lost is precisely the length of the path between x and y in the original tree. We are interested to know the asymptotics for this length when x and y are chosen at random. The largest path in a graph is called the diameter, and in practice if we are just interested in orders of magnitude, we might as well assume diameter and expected path length are the same.

So we want to know the asymptotic diameter of a UST on n vertices for large n. This is generally taken to be n^{1/2}. Here’s a quick but very informal argument that did genuinely originate on the back of a napkin. I’m using the LERW definition. Let’s start at vertex x and perform LERW, and record how long the resultant path is as time t advances. This is a Markov chain: call the path length at time t X_t.

Then if X_t=k, with probability 1-\frac k n we get X_{t+1}=k+1, and for each j in {0,…,k-1}, with probability 1/n we have X_{t+1}=j, as this corresponds to hitting a vertex we have already visited. So

\mathbb{E}\Big[X_{t+1}|X_t=k\Big]=\frac{nk-k^2/2}{n}.

Note that this drift is positive for k<< \sqrt n and negative for k>>\sqrt n, so we would expect n^{-1/2} to be the correct scaling if we wanted to find an equilibrium distribution. And the expected hitting time of vertex y is n, by a geometric distribution argument, so in fact we would expect this Markov chain to be well into the equilibrium window with the n^{-1/2} scaling by the time this occurs. As a result, we expect the length of the x to y path to have magnitude n^{1/2}, and assume that the diameter is similar.

So this will be helpful for calculations in the cycle deletion model, provided that the trees look like uniform trees. But does that even matter? Do all sensible models of random trees have diameter going like n^{1/2}? Well, a recent paper of Addario-Berry, Broutin and Reed shows that this is not the case for the minimum spanning tree. They demonstrate that the diameter in this case is n^{1/3}. I found this initially surprising, so tried a small example to see if that shed any light on the situation.

The underlying claim is that MSTs are more likely to be ‘star-like’ than USTs, a term I am not going to define. Let’s consider n=4. Specifically, consider the 4-star with centre labelled as 1. There are six possible edges in K_4 and we want to see how many of the 6! weight allocations lead to this star. If the three edges into vertex 1 have weights 1, 2 and 3 then we certainly get the star, but we can also get this star if the edges have weights 1, 2 and 4, and the edge with weight 3 lies between the edges with weights 1 and 2. So the total number of possibilities for this is 3! x 3! + 3! x 2! = 48. Whereas to get a 4-path, you can assign weights 1, 2 and 3 to the edges of the path, or weights 1, 2 and 4 provided the 4 is not in the middle, and then you have the 3 joining up the triangle formed by 1 and 2. So the number of possibilities for this is 3! x 3! + 4 x 2! = 44.

To summarise in a highly informal way, in a star-like tree, you can ‘hide’ some fairly low-scoring weights on edges that aren’t in the tree, so long as they join up very low-scoring edges that are in the tree. Obviously, this is a long way from getting any formal results on asymptotics, but it does at least show that we need to be careful about diameters if we don’t know exactly what mechanism is generating the tree!

Related articles

Minimum Spanning Trees

Posted on by
2

In my last post, I discussed the Uniform Spanning Tree. To summarise very briefly, given a connected graph on n vertices, a tree is a subgraph, that is a subset of the edges, which is connected, but which contains no cycles. It turns out this requires the tree to have n-1 edges.

We are interested in natural mechanisms for generating randomly chosen spanning trees of a given graph. One way we can always do this is to choose uniformly at random from the set of possible trees. This UST is in some sense canonical, but it is worth knowing about some other measures on trees that might be of interest.

A family of natural problems in operations research concerns an arbitrary complex network, with some weight or cost associated to each connection. The question is how to perform some operation on the network so as to minimise the resulting cost. Perhaps the most famous such problem is that of the Travelling Salesman. The story is that a salesman needs to visit n locations and wants to do the trip as efficiently as possible. This might be thought of as some sort of financial or time cost, but proably the easiest way to set it up is to imagine he is trying to minimise the distance he has to travel. It is not hard to see why this problem might genuinely arise in plenty of real-world situations, where a organisation or agent is trying to be as efficient as possible.

It might be the case that it is not possible to travel between every pair of locations, but we needn’t assume that for now. So if he knows the distance between any pair of cities, he wants to know which of the possible routes gives the shortest overall distance. The problem is that there are n! routes, and this grows roughly like n^n, which is faster than exponential, so for as few as 20 cities it has turned into a comparison which is too large to compute.

There are various algorithms which reduce the number of routes that must be checked, and some approximation methods. But if you want the exact answer, it is not currently possible to calculate this in polynomial time.

Minimal Spanning Trees and Uniqueness

For the travelling salesman, we were looking for the minimal cost spanning path. In the case of the complete graph, this is the same as the minimal cost non-repeating path of length n-1. Such paths are a subset of the set of spanning trees on the underlying graph. So what if we look instead for the minimal cost spanning tree? This exists as after all, there are only finitely many spanning trees.

So far, this has been deterministic, but we were looking for a random spanning tree. We can achieve this by choosing the weights at random. Anything other than assigning the weights as an IID sequence seems likely to be complicated, but there isn’t a canonical choice of the distribution of the weights. Our first question will be whether the distribution of the weights affects the distribution of the induced MST. In fact it will turn out that so long as the distribution is continuous, it has no effect on the distribution of the MST. The continuous condition might seem odd, but it is present only to ensure that the weights almost certainly end up generating a unique MST.

It turns out that there is a straightforward greedy algorithm to find the MST once the weights are known. We will examine some consequences of this algorithm in the random setting. First we check uniqueness. The condition required for uniqueness is that the weights be distinct. Note that this is slightly weaker than the statement that all of sums of (n-1)-tuples be distinct, which immediately implies a unique MST.

We now prove this condition. Suppose we have distinct weights, and an associated MST. If the underlying graph is a tree, then the result is clear. Otherwise, add some extra edge e, with weight w(e). By the definition of a tree, this generates exctly one cycle. Consider the other edges, say e_1,\ldots,e_k in this cycle. If any of w(e_i)>w(e) then we can replace e_i with e to get a spanning tree with smaller weight, a contradiction of the claim that we started with an MST. So by distinctness of weights, we conclude that w(e)>w(e_i) for all i.

Conversely, suppose we remove some edge e which IS in the MST. We end up with exactly two connected components. Consider all the edges in the underlying graph between the two components, and suppose that one of these f satisfies w(f)<w(e). Then if we add in edge f, which is by construction not in the original MST, we end up with a smaller total weight than we started with, a further contradiction.

We can summarise this in a neat form. Given an edge e between x and y, consider the set of all edges in the underlying graph with weight LESS THAN w(e). Then if x and y are in different components, the edge e must be in the MST. Since we have an explicit description of which edges are present, it follows that the MST is unique. The problem is that working out the component structure of the graph with higher weights removed is computationally rather intensive. We want a slightly faster algorithm.

Kruskal’s Algorithm

Several rather similar algorithms were developed roughly simultaneously. Prim’s algorithm is a slight generalisation of what we will discuss. Anyway, for now we consider Kruskal’s algorithm which has the advantage that it can be described without really needing to draw a diagram.

We start by ordering the weights. Without loss of generality, we might as well relabel the edges so that

w(e_1)< w(e_2)<\ldots< w(e_{|E|}).

Now, by the condition derived in the argument for uniqueness, we must have e_1 and e_2 in any MST. Now consider e_3. Unless doing so would create a cycle, add e_3. Then, unless doing so would create a cycle, add e_4. Continue. It is clear that the result of this procedure is acyclic. To check it is actually a spanning tree, we show that it is also connected. Suppose not, and two of the components are A and B. Let e be the edge between A and B with minimal weight. According to the algorithm, we should have included e in our MST because at no point would adding it possibly have created a cycle. So we have proved that this greedy algorithm does indeed give the (unique) MST.

A useful consequence of this is that we know the two edges with overall minimum weight are definitely in the MST. In the search for a random measure on spanning trees, what is most important is that we didn’t use the actual values of the weights in this construction, only the order. In other words, we might as well have assumed the weights were a random permutation from S_{|E|}. This now answers our original question about how the random weight MST depends in distribution on the underlying edge weight distribution. So long as with probability one the weights are distinct (which holds if the distribution is continuous), then the distribution of the resulting spanning tree is constant.

It’s not too hard to show this isn’t the same as UST: n=4 suffices as a counterexample. But the difference in asymptotic behaviour of properties such as the diameter is of interest, and will be explored in the next post.

Related articles

Uniform Spanning Trees

Posted on by
7

For applications to random graphs, the local binomial structure and independence means that the Galton-Watson branching process is a useful structure to consider embedding in the graph. In several previous posts, I have shown how we can set up the so-called exploration process which visits the sites in a component as if the component were actually a tree. The typical degree is O(1), and so in particular small components will be trees with high probability in the limit. In the giant component for a supercritical graph, this is not the case, but it doesn’t matter, as we ignore vertices we have already explored in our exploration process. We can consider the excess edges separately by ‘sprinkling’ them back in once we have the tree-like backbone of all the components. Again, independence is crucial here.

I am now thinking about a new model. We take an Erdos-Renyi process as before, with edges arriving at some fixed rate, but whenever a cycle appears, we immediately delete all the edges that make up the cycle. Thus at all times the system consists of a collection (or forest) of trees on the n vertices. So initially this process will look exactly like the normal E-R process, but as soon as the components start getting large, we start getting excess edges which destroy the cycles and make everything small again. The question to ask is: if we run the process for long enough, roughly how large are all the components? It seems unlikely that the splitting mechanism is so weak that we will get true giant components forming, ie O(n) sizes, so we might guess that, in common with some other split-merge models of this type, we end up with components of size n^{2/3}, as in the critical window for the E-R process.

In any case, the scaling limit process is likely to have components whose sizes grow with n, so we will have a class of trees larger than those we have considered previously, which have typically been O(1). So it’s worth thinking about some ways to generate random trees on a fixed number of vertices.

Conditioned Galton-Watson

Our favourite method of creating trees is inductive. We take a root and connect the root to a number of offspring given by a fixed distribution, and each of these some offspring given by an independent sample from the same distribution and so on. The natural formulation gives no control over the size of the tree. This is a random variable whose distribution depends on the offspring distribution, and which in some circumstances be computed explicitly, for example when the offspring distribution is geometric. In other cases, it is easier to make recourse to generating functions or to a random walk analogue as described in the exploration process discussion.

Of course, there is nothing to stop us conditioning on the total size of the population. This is equivalent to conditioning on the hitting time of -1 for the corresponding random walk, and Donsker’s theorem gives several consequences of a convergence relation towards a rescaled Brownian excursion. Note that there is no a priori labelling for the resulting tree. This will have to be supplied later, with breadth-first and depth-first the most natural choices, which might cause annoyance if you actually want to use it. In particular, it is not obvious, and probably not true unless you are careful, that the distribution is invariant under permuting the labels (having initially assumed 1 is the root etc) which is not ideal if you are embedding into the complete graph.

However, we would like to have some more direct constructions of random trees on n vertices. We now consider perhaps the two best known such methods. These are of particular interest as they are applicable to finding random spanning trees embedded in any graph, rather than just the complete graph.

Uniform Spanning Tree

Given a connected graph, consider the set of all subgraphs which are trees and span the vertex set of the original graph. An element of this set is called a spanning tree. A uniform spanning tree is chosen uniformly at random from the set of spanning trees on the complex graph on n vertices. A famous result of Arthur Cayley says that the number of such spanning trees is n^{n-2}. There are various neat proofs, many of which consider a mild generalisation which gives us a more natural framework for using induction. This might be a suitable subject for a subsequent post.

While there is no objective answer to the question of what is the right model for random trees on n vertices, this is what you get from the Erdos-Renyi process. Formally, conditional on the sizes of the (tree) components, the structures of the tree components are given by UST.

To see why this is the case, observe that when we condition that a component has m vertices and is a tree, we are demanding that it be connected and have m-1 edges. Since the probability of a particular configuration appearing in G(n,p) is a function only of the number of edges in the configuration, it follows that the probability of each spanning tree on the m vertices in question is equal.

Interesting things happen when you do this dynamically. That is, if we have two USTs of sizes m and n at some time t, and condition that the next edge to be added in the process joins them, then the resulting component is not a UST on m+n vertices. To see why, consider the probability of a ‘star’, that is a tree with a single distinguished vertex to which every other vertex is joined. Then the probability that the UST on m vertices is a star is \frac{m}{m^{m-2}}=m^{-(m-3)}. By contrast, it is not possible to obtain a star on m+n vertices by joining a tree on m vertices and a tree on n vertices with an additional edge.

However, I think the UST property is preserved by the cycle deletion mechanism mentioned at the very start of this post. My working has been very much of the back of the envelope variety, but I am fairly convinced that once you have taken a UST and conditioned on the sizes of the smaller trees which result from cycle deletion. My argument is that you might as well fix the cycle to be deleted, then condition on how many vertices are in each of the trees coming off this cycle. Now the choice of each of these trees is clearly uniform among spanning trees on the correct number of vertices.

However, it is my current belief that the combination of these two mechanisms does not give UST-like trees even after conditioning on the sizes at fixed time.

Related articles