Lecture 8 – Bounds in the critical window

Posted on March 23, 2019 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

Preliminary – positive correlation, Harris inequality

I wrote about independence, association, and the FKG property a long time ago, while I was still an undergraduate taking a first course on Percolation in Cambridge. That post is here. In the lecture I discussed the special case of the FKG inequality applied in the setting of product measure setting, of which the Erdos-Renyi random graph is an example, and which is sometimes referred to as the Harris inequality.

Given two increasing events A and B, say for graphs on [n], then if $\mathbb{P}$ is product measure on the edge set, we have

$\mathbb{P}(A\cap B)\ge \mathbb{P}(A)\mathbb{P}(B).$

Intuitively, since both A and B are ‘positively-correlated’ with the not-rigorous notion of ‘having more edges’, then are genuinely positively-correlated with each other. We will use this later in the post, in the form $\mathbb{E}[X|A]\ge \mathbb{E}[X]$ , whenever X is an increasing RV and A is an increasing event.

The critical window

During the course, we’ve discussed separately the key qualitative features of the random graph $G(n,\frac{\lambda}{n})$ in the

subcritical regime when $\lambda<1$ , for which we showed that all the components are small, in the sense that $\frac{1}{n}|L_1| \stackrel{\mathbb{P}}\rightarrow 0$ , although the same argument would also give $|L_1|\le K\log n$ with high probability if we used stronger Chernoff bounds;
supercritical regime when $\lambda>1$ , for which there is a unique giant component , ie that $\frac{1}{n}|L_1|\stackrel{\mathbb{P}}\rightarrow \zeta_\lambda>0$ , the survival probability of a Galton-Watson branching process with Poisson( $\lambda$ ) offspring distribution. Arguing for example by a duality argument shows that with high probability all other components are small in the same sense as in the subcritical regime.

In between, of course we should study $G(n,\frac{1}{n})$ , for which it was known that $L_1\stackrel{d}\sim n^{2/3},\, L_2\stackrel{d}\sim n^{2/3},\ldots$ . (*) That is, the largest components are on the scale $n^{2/3}$ , and there are lots of such critical components.

In the early work on random graphs, the story ended roughly there. But in the 80s, these questions were revived, and considerable work by Bollobas and Luczak, among many others, started investigating the critical setting in more detail. In particular, between the subcritical and the supercritical regimes, the ratio $\frac{|L_2|}{|L_1|}$ between the sizes of the largest and second-largest components goes from ‘concentrated on 1’ to ‘concentrated on 0’. So it is reasonable to ask what finer scaling of the edge probability $p(n)$ around $\frac{1}{n}$ should be chosen to see this transition happen.

Critical window

In this lecture, we studied the critical window, describing sequences of probabilities of the form

$p(n)=\frac{1+\lambda n^{-1/3}}{n},$

where $\lambda\in(-\infty,+\infty)$ . (Obviously, this is a different use of $\lambda$ to previous lectures.)

It turns out that as we move $\lambda$ from $-\infty$ to $+\infty$ , this window gives exactly the right scaling to see the transition of $\frac{|L_2|}{|L_1|}$ described above. Work by Bollobas and Luczak and many co-authors and others in the 80s establish a large number of results in this window, but for the purposes of this course, this can be summarised as saying that the critical window has the same scaling behaviour as $p(n)=1/n$ , with a large number of components on the scale $\sim n^{2/3}$ (see (*) earlier), but different scaling limits.

Note: Earlier in the course, we have discussed local limits, in particular for $G(n,\lambda/n)$ , where the local limit is a Galton-Watson branching process tree with offspring distribution $\mathrm{Poisson}(\lambda)$ . Such local properties are not sufficient to distinguish between different probabilities within the critical window. Although there are lots of critical components, it remains the case that asymptotically almost all vertices are in ‘small components’.

The precise form of the scaling limit for

$\frac{1}{n^{2/3}} \left( |L_1|, |L_2|, |L_3|,\ldots \right)$

as $n\rightarrow\infty$ was shown by Aldous in 1997, by lifting a scaling limit result for the exploration process, which was discussed in this previous lecture and this one too. Since Brownian motion lies outside the assumed background for this course, we can’t discuss that, so this lecture establishes upper bounds on the correct scale of $|L_1|$ in the critical window. Continue reading →

Lecture 10 – the configuration model

Posted on January 15, 2019 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

As we enter the final stages of the semester, I want to discuss some extensions to the standard Erdos-Renyi random graph which has been the focus of most of the course so far. Although we will not get far into the details during this course, the overall goal is to develop models which are close to Erdos-Renyi in terms of ease of analysis, while also allowing more of the features characteristic of networks observed in the real world.

One of the more obvious deficiencies of the sparse regime of Erdos-Renyi random graphs for modelling ‘real-world phenomena’ concerns the degree sequence. Indeed, the empirical degree distribution of G(n,c/n) converges to Poisson(c). By contrast, in real-world networks, a much wider range of degrees is typically observed, and in many cases it is felt that these should follow a power law, with a small number of a very highly connected agents.

One way around this problem to construct random graphs where we insist that the graph has a given sequence of degrees. The configuration model, which is the subject of this lecture and this post (and about which I’ve written before), offers one way to achieve this.

Definition and notes

Let $n\ge 1$ and let $d=(d_1,d_2,\ldots,d_n)$ be a sequence of non-negative integers such that $\sum_{i=1}^n d_i$ is even. Then the configuration model with degree sequence d is a random multigraph with vertex set [n], constructed as follows:

To each vertex $i\in[n]$ , assign $d_i$ half-edges;
Then, take a uniform matching of these half-edges;
Finally, for each pair of half-edges in the matching, replace the two half-edges with a genuine edge, to obtain the multigraph $CM_n(d)$ , in which, by construction, vertex i has degree $d_i$ .

One should note immediately that although the matching is uniform, the multigraph is not uniform amongst multigraphs with that degree sequence. Note also that the condition on the sums of the degrees is necessary for any graph, and in this context means that the number of half-edges is even, without which it would not be possible to construct a matching.

This effect is manifest in the simplest possible example, when n=2 and d=(3,3). There are two possible graphs, up to isomorphism, which are shown below:

For obvious reasons, we might refer to these as the handcuffs and the theta , respectively. It’s helpful if we, temporarily, assume the half-edges are distinguishable at the moment we join them up in the configuration model construction. Because then there are 3×3=9 ways to join them up to form the handcuffs (think of which half-edge ends up forming the edge between the two vertices) while there are 3!=6 ways to pair up the half-edges in the theta.

In general, for multigraphs H with the correct degree sequence, we have

$\mathbb{P}( CM_n(d)\simeq H) \propto \left( 2^{\# \text{loops}(H)} \prod_{e\in E(H)} \text{mult}(e)! \right),$

where $\text{mult}(e)$ is the multiplicity with which a given edge e appears in H.

Note: it might seem counterintuitive that this procedure is biased against multiple edges and self-loops, but it is really just saying that there are more ways to form two distinct edges than to form two equal edges (ie a multiedge pair) when we view the half-edges as distinguishable. (See this post for further discussion of this aspect in the 3-regular setting.)

However, a consequence of this result is that if we condition on the event that $CM_n(d)$ is simple, then the resulting random graph is uniform on the set of simple graphs satisfying the degree property. Note that the same example as above shows that there’s no guarantee that there exists a simple graph whose degrees are some given sequence.

d-regular configuration model

In general, from a modelling point of view, we are particularly interested in simple, connected graphs, and so it is valuable to study whether the large examples of the configuration model are likely to have these properties. In this lecture, I will mainly focus on the case where the multigraphs are d-regular, meaning that all the vertices have degree equal to d. For the purposes of this lecture, we denote by $G^d(n)$ , the d-regular configuration model $CM_n(d,\ldots,d)$ .

d=1: to satisfy the parity condition on the sums of degrees, we must have n even. But then $G^1(n)$ will consist of n/2 disjoint edges.
d=2: $G^2(n)$ will consist of some number of disjoint cycles, and it is a straightforward calculation to check that when n is large, with high probability the graph will be disconnected.

In particular, I will focus on the case when d=3, which is the first interesting case. Most of the results we prove here can be generalised (under various conditions) to more general examples of the configuration model. The main goal of the lecture is revision of some techniques of the course, plus one new one, in a fresh setting, and the strongest possible versions of many of these results can be found amongst the references listed at the end.

Connectedness

In the lecture, we showed that $G^3(2n)$ is connected with high probability. This is, in fact, a very weak result, since in fact $G^d(n)$ is d-connected with high probability for $d\ge 3$ [Bol81, Wor81]. Here, d-connected means that one must remove at least d vertices in order to disconnect the graph, or, equivalently, that there are d disjoint paths between any pair of vertices. Furthermore, Bollobas shows that for $d\ge 3$ , $G^d(n)$ is a (random) expander family [Bol88].

Anyway, for the purposes of this course, the main tool is direct enumeration. The matching number $M_{2k}$ satisfies

$M_{2k}=(2k-1)\times (2k-3)\times\ldots\times 3\times 1 = \frac{(2k)!}{2^k \cdot k!},$

and so Stirling’s approximation gives the asymptotics

$M_{2k} = (\sqrt{2}+o(1)) \left(\frac{2}{e}\right)^k k^k,$

although it will be useful to use the true bounds

$c \left(\frac{2}{e}\right)^k k^k \le M_{2k}\le C\left(\frac{2}{e}\right)^k k^k,\quad \forall k,$

instead in some places. Anyway, in $G^3(2n)$ , there are 6n half-edges in total, and so the probability that the graph may be split into two parts consisting of $2\ell,2m$ vertices, with $2\ell+2m=2n$ , and with no edges between the classes is $\frac{\binom{2n}{2\ell} M_{6\ell}M_{6m}}{M_{6n}}.$ Continue reading →

Lecture 9 – Inhomogeneous random graphs

Posted on January 8, 2019 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

As we enter the final stages of the semester, I want to discuss some extensions to the standard Erdos-Renyi random graph which has been the focus of most of the course so far. In doing so, we can revisit material that we have already covered, and discover how easily one can extend this directly to more exotic settings.

The focus of this lecture was the model of inhomogeneous random graphs (IRGs) introduced by Soderberg [Sod02] and first studied rigorously by Bollobas, Janson and Riordan [BJR07]. Soderberg and this blog post address the case where vertices have a type drawn from a finite set. BJR address the setting with more general typespaces, in particular a continuum of types. This generalisation is essential if one wants to use IRGs to model effects more sophisticated than those of the classical Erdos-Renyi model G(n,c/n), but most of the methodology is present in the finite-type setting, and avoids the operator theory language which is perhaps intimidating for a first-time reader.

Inhomogeneous random graphs

Throughout, $k\ge 2$ is fixed. A graph with k types is a graph G=(V,E) together with a type function $V\to \{1,\ldots,k\}$ . We will refer to a $k\times k$ symmetric matrix with non-negative entries as a kernel.

Given $n\in\mathbb{N}$ and a vector $p=(p_1,\ldots,p_k)\in\mathbb{N}_0^k$ satisfying $\sum p_i=n$ , and $\kappa$ a kernel, we define the inhomogeneous random graph $G^n(p,\kappa)$ with k types as:

the vertex set is [n],
types are assigned uniformly at random to the vertices such that exactly $p_i$ vertices have type i.
Conditional on these types, each edge $v\leftrightarrow w$ (for $v\ne w\in [n]$ ) is present, independently, with probability

$1 - \exp\left(-\frac{\kappa_{\mathrm{type}(v),\mathrm{type}(w)} }{n} \right).$

Notes on the definition:

Alternatively, we could assign the types so that vertices $\{1,\ldots,p_1\}$ have type 1, $\{p_1+1,\ldots,p_1+p_2\}$ have type 2, etc etc. This makes no difference except in terms of the notation we have to use if we want to use exchangeability arguments later.
An alternative model considers some distribution $\pi$ on [k], and assigns the types of the vertices of [n] in an IID fashion according to $\pi$ . Essentially all the same results hold for these two models. (For example, this model with ‘random types’ can be studied by quenching the number of each type!) Often one works with whichever model seems easier for a given proof.
Note that the edge probability given is $\approx \frac{\kappa_{\mathrm{type}(v),\mathrm{type}(w)}}{n}$ . The exponential form has a more natural interpretation if we ever need to turn the IRGs into a process. Additionally, it avoids the requirement to treat small values of n (for which, a priori, $k/n$ might be greater than 1) separately.

In the above example, one can see that, roughly speaking, red vertices are more likely to be connected to each other than blue vertices. However, for both colours, they are more likely to be connected to a given vertex of the same colour than a vertex of the opposite colour. This might, for example, correspond to the kernel $\begin{pmatrix}3&1\\1&2\end{pmatrix}$ .

The definition given above corresponds to a sparse setting, where the typical vertex degrees are $\Theta(1)$ . Obviously, one can set up an inhomogeneous random graph in a dense regime by an identical argument.

From an applications point of view, it’s not hard to imagine that an IRG of some flavour might be a good model for many phenomena observed in reality, especially when a mean-field assumption is somewhat appropriate. The friendships of boys and girls in primary school seems a particularly resonant example, though doubtless there are many others.

One particular application is to recover the types of the vertices from the topology of the graph. That is, if you see the above picture without the colours, can you work out which vertices are red, and which are blue? (Assuming you know the kernel.) This is clearly impossible to do with anything like certainty in the sparse setting – how does one decide about isolated vertices, for example? The probabilities that a red vertex is isolated and that a blue vertex is isolated differ by a constant factor in the $n\rightarrow\infty$ limit. But in the dense setting, one can achieve this with high confidence. When studying such statistical questions, these IRGs are often referred to as stochastic block models, and the recent survey of Abbe [Abbe] gives a very rich history of this type of problem in this setting.

Poisson multitype branching processes

As in the case of the classical random graph G(n,c/n), we learn a lot about the IRG by studying its local structure. Let’s assume from now on that we are given a sequence of IRGs $G^n(p^n,\kappa)$ for which $\frac{p^n}{n}\rightarrow \pi$ , where $\pi=(\pi_1,\ldots,\pi_k)\in[0,1]^k$ satisfies $||\pi||_1=1$ .

Now, let $v^n$ be a uniformly-chosen vertex in [n]. Clearly $\mathrm{type}(v^n)\stackrel{d}\rightarrow \pi$ , with the immediate mild notation abuse of viewing $\pi$ as a probability distribution on [k].

Then, conditional on $\mathrm{type}(v^n)=i$ :

when $j\ne i$ , the number of type j neighbours of $v^n$ is distributed as $\mathrm{Bin}\left(p_j,1-\exp\left(-\frac{\kappa_{i,j}}{n}\right)\right)$ .
the number of type i neighbours of $v^n$ is distributed as $\mathrm{Bin}\left( p_i-1,1-\exp\left(-\frac{\kappa_{i,i}}{n}\right)\right)$ .

Note that $p_j\left[1-\exp\left(-\frac{\kappa_{i,j}}{n}\right)\right]\approx \frac{p_j\cdot \kappa_{i,j}}{n} \approx \kappa_{i,j}\pi_j$ , and similarly in the case j=i, so in both cases, the number of neighbours of type j is distributed approximately as $\mathrm{Poisson}(\kappa_{i,j}\pi_j)$ .

This motivates the following definition of a branching process tree, whose vertices have k types. Continue reading →

Lecture 7 – The giant component

Posted on December 15, 2018 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

As we edge into the second half of the course, we are now in a position to return to the question of the phase transition between the subcritical regime $\lambda<1$ and the supercritical regime $\lambda>1$ concerning the size of the largest component $L_1(G(n,\lambda/n))$ .

In Lecture 3, we used the exploration process to give upper bounds on the size of this largest component in the subcritical regime. In particular, we showed that

$\frac{1}{n}\big| L_1(G(n,\lambda/n)) \big| \stackrel{\mathbb{P}}\rightarrow 0.$

If we used slightly stronger random walk concentration estimates (Chernoff bounds rather than 2nd-moment bounds from Chebyshev’s inequality), we could in fact have shown that with high probability the size of this largest component was at most some logarithmic function of n.

In this lecture, we turn to the supercritical regime. In the previous lecture, we defined various forms of weak local limit, and asserted (without attempting the notationally-involved combinatorial calculation) that the random graph $G(n,\lambda/n)$ converges locally weakly in probability to the Galton-Watson tree with $\text{Poisson}(\lambda)$ offspring distribution, as we’ve used informally earlier in the course.

Of course, when $\lambda>1$ , this branching process has strictly positive survival probability $\zeta_\lambda>0$ . At a heuristic level, we imagine that all vertices whose local neighbourhood is ‘infinite’ are in fact part of the same giant component, which should occupy $(\zeta_\lambda+o_{\mathbb{P}}(1))n$ vertices. In its most basic form, the result is

$\frac{1}{n}\big|L_1(G(n,\lambda/n))\big|\;\stackrel{\mathbb{P}}\longrightarrow\; \zeta_\lambda,\quad \frac{1}{n}\big|L_2(G(n,\lambda/n))\big| \;\stackrel{\mathbb{P}}\longrightarrow\; 0,$ (*)

where the second part is a uniqueness result for the giant component.

The usual heuristic for proving this result is that all ‘large’ components must in fact be joined. For example, if there are two giant components, with sizes $\approx \alpha n,\approx \beta n$ , then each time we add a new edge (such an argument is often called ‘sprinkling‘), the probability that these two components are joined is $\approx 2ab$ , and so if we add lots of edges (which happens as we move from edge probability $\lambda-\epsilon\mapsto \lambda$ ) then with high probability these two components get joined.

It is hard to make this argument rigorous, and the normal approach is to show that with high probability there are no components with sizes within a certain intermediate range (say between $\Theta(\log n)$ and $n^\alpha$ ) and then show that all larger components are the same by a joint exploration process or a technical sprinkling argument. Cf the books of Bollobas and of Janson, Luczak, Rucinski. See also this blog post (and the next page) for a readable online version of this argument.

I can’t find any version of the following argument, which takes the weak local convergence as an assumption, in the literature, but seems appropriate to this course. It is worth noting that, as we shall see, the method is not hugely robust to adjustments in case one is, for example, seeking stronger estimates on the giant component (eg a CLT).

Anyway, we proceed in three steps:

Step 1: First we show, using the local limit, that for any $\epsilon>0$ ,

$\frac{1}{n}\big|L_1(G(n,\lambda/n))\big| \le \zeta_\lambda+\epsilon,$ with high probability as $n\rightarrow\infty$ .

Step 2: Using a lower bound on the exploration process, for $\epsilon>0$ small enough

$\frac{1}{n}\big|L_1(G(n,\lambda/n))\big| \ge \epsilon,$ with high probability.

Step 3: Motivated by duality, we count isolated vertices to show

$\mathbb{P}(\epsilon n\le |L_1| \le (\zeta_\lambda-\epsilon)n) \rightarrow 0.$

We will return to uniqueness at the end.

Step 1

This step is unsurprising. The local limit gives control on how many vertices are in small components of various sizes, and so gives control on how many vertices are in small components of all finite sizes (taking limits in the right order). This gives a bound on how many vertices can be in the giant component. Continue reading →

Lecture 6 – Local limits

Posted on December 4, 2018 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

By this point of the course, we’ve studied several aspects of the Erdos-Renyi random graph, especially in the sparse setting $G(n,\frac{\lambda}{n})$ . We’ve also taken a lengthy detour to revise Galton-Watson trees, with a particular focus on the case of Poisson offspring distribution.

This is deliberate. Note that a given vertex v of $G(n,\frac{\lambda}{n})$ has some number of neighbours distributed as $\mathrm{Bin}(n-1,\frac{\lambda}{n})\stackrel{d}\approx\mathrm{Po}(\lambda)$ , and the same approximation remains valid as we explore the graph (for example in a breadth-first fashion) either until we have seen a large number of vertices, or unless some ultra-pathological event happens, such as a vertex having degree n/3.

In any case, we are motivated by the notion that the local structure of $G(n,\frac{\lambda}{n})$ is well-approximated by the Galton-Watson tree with $\mathrm{Po}(\lambda)$ offspring, and in this lecture and the next we try to make this notion precise, and discuss some consequences when we can show that this form of convergence occurs.

Deterministic graphs

Throughout, we will be interested in rooted graphs, since by definition we have to choose a root vertex whose local neighbourhood is to be studied. Usually, we will study a sequence of rooted graphs $(G_n,\rho_n)$ , where the vertex set of $G_n$ is [n], or certainly increasing in n (as in the first example).

For some rooted graph $(G,\rho)$ , we say such a sequence $(G_n,\rho_n)$ converges to $(G,\rho)$ locally if for all radii $r\ge 1$ , we have $B_r^{G_n}(\rho_n)\simeq B_r^G(\rho)$ . In words, the neighbourhood around $\rho_n$ in $G_n$ is the same up to radius r as the neighbourhood around $\rho$ in $G$ , so long as n is large enough (for given r).

This is best illustrated by an example, such as $T_n$ , the binary tree to depth n.

If we take $\rho_n$ to be the usual root, then the trees are nested, and converge locally to the infinite binary tree $T_\infty$ . Slightly less obviously, if we take $\rho_n$ to be one of the leaves, then the trees are still nested (up to labelling – ie in the sense of isomorphisms of rooted trees), and converge locally to the canopy tree, defined by a copy of $\mathbb{Z}_{\ge 0}$ with nearest-neighbour edges, and where each vertex $n\ge 1$ is connected to the root of a disjoint copy of $T_{n-1}$ , as shown below:

Things get more interesting when the root is chosen randomly, for example, uniformly at random, as this encodes more global information about the graphs $G_n$ . In the case where the $G_n$ are vertex-transitive, then if we only care about rooted graphs up to isomorphism, then it doesn’t matter how we choose the root.

Otherwise, we say that $G_n$ converges in the local weak sense to $(G,\rho)$ if, for all $r\ge 1$ and for all rooted graphs $(H,\rho_H)$ ,

$\mathbb{P}\left( B^{G_n}_r(\rho_n)\simeq (H,\rho_H) \right) \longrightarrow \mathbb{P}\left( B_r^G(\rho)\simeq H\right),$

as $n\rightarrow\infty$ .

Alternatively, one can phrase this as a result about convergence of rooted-graph-valued distributions.

A simple non-transitive example is $G_n\simeq P_n$ , the path of length n. Then, the r-neighbourhood of a vertex is isomorphic to $P_{2r}$ , unless that vertex is within graph-distance (r-1) of one of the leaves of $G_n$ . As $n\rightarrow\infty$ , the proportion of such vertices vanishes, and so, $\mathbb{P}\left( B^{P_n}_r(\rho_n)\simeq P_{2r}\right)\rightarrow 1$ , from which we conclude the unsurprising result that $P_{n}$ converges in the local weak sense to $\mathbb{Z}$ . (Which is vertex-transitive, so it doesn’t matter where we select the root.)

The binary trees offer a slightly richer perspective. Let $\mathcal{L}_n$ be the set of leaves of $T_n$ , and we claim that when $\rho_n$ is chosen uniformly from the vertices of $T_n$ , then $d_{T_n}(\rho_n,\mathcal{L}_n)$ converges in distribution. Indeed, $\mathbb{P}\left( d_{T_n}(\rho_n,\mathcal{L}_n)=k\right) = \frac{2^{n-k}}{2^{n+1}-1}$ , whenever $n\ge k$ , and so the given distance converges in distribution to the Geometric distribution with parameter 1/2 supported on {0,1,2,…}.

This induces a random local weak limit, namely the canopy tree, rooted at one of the vertices we denoted by $\mathbb{Z}_{\ge 0}$ , with the choice of this vertex given by Geometric(1/2). Continue reading →

Lecture 4 – Hitting time theorem

Posted on December 1, 2018 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

This lecture consisted of revision of the most relevant theory of Galton-Watson trees, with a focus on the case where the offspring distribution is Poisson, since, as we have seen in previous lectures, this is a strong candidate to approximate the structure of $G(n,\lambda/n)$ . It makes sense to cover the theory of the trees before attempting to make rigorous the sense of approximation.

Given a Galton-Watson tree T, it is natural to label the vertices in a breadth-first order as $\varnothing=v_1,v_2,\ldots,v_{|T|}$ . This is easiest if we have constructed the Galton-Watson tree as a subset of the infinite Ulam-Harris tree, where vertices have labels like (3,5,17,4), whose parent is (3,5,17). If this child vertex is part of the tree, then so are (3,5,17,1), (3,5,17,2), and (3,5,17,3). This means our breadth-first order is canonically well-defined, as we have a natural ordering of the children of each parent vertex.

Note: one advantage of using breadth-first order rather than depth-first order (which corresponds to the usual dictionary, or lexicographic ordering of the labels) is that if the tree is infinite, we don’t explore all of it during a depth-first search. (In the sense that there exist vertices which are never given a finite label.) For breadth-first search, a similar problem arises precisely when some vertex has infinitely many children. For a conventional Galton-Watson tree, the latter situation is much less of a problem than the infinite total population problem, which happens with positive probability whenever $\mu=\mathbb{E}[X]>1$ .

Anyway, given the depth-first order, one can consider an exploration process $S_0,S_1,S_2,\ldots,S_{|T|}$ given by

$S_0=1,\quad S_i=S_{i-1}+(X_i-1),$

where $X_i$ is the number of children of $v_i$ . In this way, we see that

$S_i=\big| \Gamma(v_1)\cup\ldots\cup\Gamma(v_i)\backslash \{v_1,\ldots,v_i\}\big|,\quad i\ge 1,$

records the number of vertices in some stack containing those which we have ‘seen but not explored’. Some authors prefer to start from 0, in which case one ends up with a similar but slightly different interpretation of the ‘stack’, but that’s fine since we aren’t going to define formally what ‘seen’ and ‘explored’ means in this post.

Essentially, we exhaust the vertices of the tree whenever $S_t=0$ , and so the condition that $|T|=n$ requires

$S_n=0,\quad S_m\ge 1,\; m=0,1,\ldots,n-1.$

Conveniently, so long as we have avoiding ordering ambiguity, for example by insisting that trees live within the Ulam-Harris tree, we can reconstruct T uniquely from $(S_0,S_1,\ldots,S_{|T|})$ .

Furthermore, if T is a Galton-Watson process, then the numbers of children $X_i$ are IID, and so in fact this exploration process is a random walk, and the size of the tree can be recovered as the hitting time of zero.

Note: making fully rigorous the argument that children in the GW tree are independent of the breadth-first walk fully rigorous is somewhat technical, and not to be dismissed lightly, though not of principle interest at the level of this topics course. See Proposition 1.5 in Section 1.2 of Le Gall’s notes or Section 1.2.2 of my doctoral thesis for further discussion and argument.

The hitting time theorem allows us to study the distribution of the hitting time of a random walk whose increments are bounded below by -1, in terms of the distribution of the value of the random walk.

Theorem: Let $(S_n,\, n\ge 0)$ be a random walk with $S_0=0$ and IID increments $(X_n,n\ge 1)$ satisfying $\mathbb{P}(X_n\ge -1)=1$ . Let $H_{-k}=\inf \left\{n\,:\, S_n=-k\right\}$ be the hitting time of -k.

Then $\mathbb{P}\big( H_{-k}=n\big) = \frac{k}{n}\mathbb{P}\big(S_n=-k)$ .

Commentary: there are local central limit theorem estimates and large deviation estimates that allow good control of the probability on the RHS for a rich class of contexts. So at a meta-level, the hitting time theorem allows us to reduce a complicated (though still classical) problem, to a real classical problem, which is particularly helpful when the LHS is a device for capturing relevant information about our random tree model.

Continue reading →

Lecture 3 – Couplings, comparing distributions

Posted on November 21, 2018 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

In this third lecture, we made our first foray into the scaling regime for G(n,p) which will be the main focus of the course, namely the sparse regime when $p=\frac{\lambda}{n}$ . The goal for today was to give a self-contained proof of the result that in the subcritical setting $\lambda<1$ , there is no giant component, that is, a component supported on a positive proportion of the vertices, with high probability as $n\rightarrow\infty$ .

More formally, we showed that the proportion of vertices contained within the largest component of $G(n,\frac{\lambda}{n})$ vanishes in probability:

$\frac{1}{n} \left| L_1\left(G\left(n,\frac{\lambda}{n}\right)\right) \right| \stackrel{\mathbb{P}}\longrightarrow 0.$

The argument for this result involves an exploration process of a component of the graph. This notion will be developed more formally in future lectures, aiming for good approximation rather than bounding arguments.

But for now, the key observation is that when we ‘explore’ the component of a uniformly chosen vertex $v\in[n]$ outwards from v, at all times the number of ‘children’ of v which haven’t already been considered is ‘at most’ $\mathrm{Bin}(n-1,\frac{\lambda}{n})$ . Since, for example, if we already know that eleven vertices, including the current one w are in C(v), then the distribution of the number of new vertices to be added to consideration because they are directly connected to w has conditional distribution $\mathrm{Bin}(n-11,\frac{\lambda}{n})$ .

Firstly, we want to formalise the notion that this is ‘less than’ $\mathrm{Bin}(n,\frac{\lambda}{n})$ , and also that, so long as we don’t replace 11 by a linear function of n, that $\mathrm{Bin}(n-11,\frac{\lambda}{n})\stackrel{d}\approx \mathrm{Poisson}(\lambda)$ .

Couplings to compare distributions

A coupling of two random variables (or distributions) X and Y is a realisation $(\hat X,\hat Y)$ on the same probability space with correct marginals, that is

$\hat X\stackrel{d}=X,\quad \hat Y\stackrel{d}=Y.$

We saw earlier in the course that we could couple G(n,p) and G(n,q) by simulating both from the same family of uniform random variables, and it’s helpful to think of this in general: ‘constructing the distributions from the same source of randomness’.

Couplings are a useful notion to digest at this point, as they embody a general trend in discrete probability theory. Wherever possible, we try to do as we can with the random objects, before starting any calculations. Think about the connectivity property of G(n,p) as discussed in the previous lecture. This can be expressed directly as a function of p in terms of a large sum, but showing it is an increasing function of p is essentially impossible by computation, whereas this is very straightforward using the coupling.

We will now review how to use couplings to compare distributions.

For a real-valued random variable X, with distribution function $F_X$ , we always have the option to couple with a uniform U(0,1) random variable. That is, when $U\sim U[0,1]$ , we have $(F_X^{-1}(U)\stackrel{d}= X$ , where the inverse of the distribution function is defined (in the non-obvious case of atoms) as

$F_X^{-1}(u)=\inf\left\{ x\in\mathbb{R}\,:\, F(x)\ge u\right\}.$

Note that when the value taken by U increases, so does the value taken by $F_X^{-1}(U)$ . This coupling can be used simultaneously on two random variables X and Y, as $(F_X^{-1}(U),F_Y^{-1}(U))$ , to generate a coupling of X and Y.

The total variation distance between two probability measures is

$d_{\mathrm{TV}}(\mu,\nu):= \sup_{A}|\mu(A)-\nu(A)|$ ,

with supremum taken over all events in the joint support S of $\mu,\nu$ . This is particularly clear in the case of discrete measures, as then

$d_{\mathrm{TV}}(\mu,\nu)=\frac12 \sum_{x\in S} \left| \mu\left(\{x\}\right) - \nu\left(\{x\}\right) \right|.$

(Think of the difference in heights between the bars, when you plot $\mu,\nu$ simultaneously as a bar graph…)

The total variation distances records how well we can couple two distributions, if we want them to be equal as often as possible. It is therefore a bad measure of distributions with different support. For example, the distributions $\delta_0$ and $\delta_{1/n}$ are distance 1 apart (the maximum) for all values of n. Similarly, the uniform distribution on [0,1] and the uniform distribution on $\{0,1/n,2/n,\ldots, n-1/n, 1\}$ are also distance 1 apart.

When there is more overlap, the following result is useful.

Proposition: Any coupling $(\hat X,\hat Y)$ of $X\sim \mu,\,Y\sim \nu$ satisfies $\mathbb{P}(X=Y)\le 1-d_{\mathrm{TV}}(\mu,\nu)$ , and there exists a coupling such that equality is achieved. Continue reading →

Lecture 2 – Connectivity threshold

Posted on November 16, 2018 by dominicyeo

I am aiming to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics for the course can be found here.

The goal of the second lecture was to establish the sharp phase transition for the connectivity of the random graph G(n,p(n)) around the critical regime $p(n)\sim \frac{\log n}{n}$ . In the end, we showed that when $\omega(n)$ is any diverging sequence, and $p(n)=\frac{\log n-\omega(n)}{n}$ , then we have that G(n,p(n)) is with high probability not connected.

In the next lecture, we will finish the classification by studying $p(n)=\frac{\log n+\omega(n)}{n}$ , and show that for this range of p, the graph G(n,p(n)) is with high probability connected.

The details of the lecture, especially the calculation, are not presented fully here. There, I followed van der Hofstad’s recent book fairly closely, sometimes taking different approximations and routes through the algebra, though all versions remain fairly close to the original enumerations by Renyi.

Immediate remarks

One is allowed to be surprised that for almost all scalings of p(n), G(n,p) is either whp connected or whp not connected. The speed of the transition is definitely interesting.
As defined in lectures, the property that a graph is connected is an increasing property, meaning that it is preserved when you add additional edges to the graph.
Because of the natural coupling between G(n,p) and G(n,q), the fact that connectedness is an increasing property makes life easier. For example, we can insist temporarily that $\omega(n)\ll \log n$ , or whatever scaling turns out to be convenient for the proof, but conclude the result for all diverging $\omega(n)$ . This avoids the necessity for an annoying case distinction.

Heuristics – Isolated vertices

It turns out that the ‘easiest’ way for such a graph to be disconnected is for it to have an isolated vertex. In determining that the graph has a cut into classes of sizes a and b with no edges between them, there is a trade-off between the number of ways to choose the partition (which increases with min(a,b) ) and the probabilistic penalty from banning the ab edges between the classes (which decreases with min(a,b) ). It turns out that the latter effect is slightly stronger, and so (1,n-1) dominates.

Method 1: second-moment method

In the case $p(n)=\frac{\log n - \omega(n)}{n}$ , we use a second-moment method argument to establish that G(n,p) contains an isolated vertex with high probability. Note that a given vertex v is isolated precisely if n-1 edges are not present. Furthermore, two given vertices v,w are both isolated, precisely if 2n-3 edges are not present. So in fact, both the first moment and the second moment of the number of isolated vertices are straightforward to evaluate.

It turns out that the number of isolated vertices, $Y_n$ , satisfies

$\mathbb{E}[Y_n]= \exp(\omega(n)+o(1))\rightarrow\infty.$ (*)

As always, we have to eliminate the possibility that this divergent expectation is achieved by the graph typically having no isolated vertices, but occasionally having very many. So we turn to the second moment, and can show

$\mathrm{Var}(Y_n)= (1+o(1))\mathbb{E}[Y_n],$

and so by Chebyshev’s inequality, we have $\mathbb{P}(Y_n=0)\rightarrow 0$ .

Method 2: first-moment method

Counter-intuitively, although the case $p(n)=\frac{\log n + \omega(n)}{n}$ requires only a first-moment method, it is more technical because it involves the non-clear direction of the informal equivalence:

$\text{Connected}\; ``\iff ''\; \text{no isolated vertices}.$

At the time we showed (*), we also showed that for this regime of p(n), G(n,p) whp has no isolated vertices. It remains to show that it has no splits into (unions of) connected components of sizes k and n-k. Continue reading →

Random Graphs – Lecture 1

Posted on November 5, 2018 by dominicyeo

My plan is to write a short post about each lecture in my ongoing course on Random Graphs. Details and logistics about the course can be found here.

In the first lecture, we revised some basic definitions about graphs, focusing on those which are most relevant to a first study of the Erdos-Renyi random graph G(n,p) which will be the focus of the lecture course. We discussed in abstract why the independence of the (potential) edges makes the model easier to analyse, but reduces its suitability as a direct model for lots of networks one might see in the real world, where knowledge that A is directly connected to both B and C affects the probability that B is directly connected to C, in either direction. Thinking about the Facebook friendship graph is one of the best examples, where in this case, we expect this extra information to increase the probability that B and C are connected. Even as the world moves away from heteronormativity, it realistically remains the case that in a graph of the dating history amongst a well-defined community we would likely observe the opposite effect.

All of these more complicated phenomena can be captured by various random graphs, but G(n,p) remains the corner stone, evinced by the $>10^5$ citations towards one of Erdos and Renyi’s original papers on the topic.

Somewhat paraphrasing, one of their (well, mostly Renyi’s) original questions was: when n is large, what should p be so that there’s a good chance that G(n,p) is connected?

The answer to this question lies in Lecture 2, but to cement understanding of the model, and explore some key methods for proofs in discrete probability (as well as play around with the big-O and little-o notation), we investigated the following two situations, which are very far from interesting as far as connectivity of G(n,p) is concerned.

Dense regime

When p is fixed, there are many interesting questions one could ask about the asymptotic properties of G(n,p), but connectivity is not one of them. In particular, for $p\in(0,1)$ we claim:

Proposition: $\mathrm{diam}(G(n,p)) \stackrel{\mathbb{P}}\rightarrow 2$ as $n\rightarrow\infty$ .

Note that if $\mathrm{diam}(G(n,p))=1$ , then $G(n,p)\simeq K_n$ , the complete graph on n vertices. In other words, every possible edge is actually present. But the probability of this event is $p^{\binom{n}{2}}\rightarrow 0$ , so long as p<1.

It then suffices to prove that $\mathbb{P}(G(n,p)>2) \rightarrow 0$ . We use a union bound, where we study the probability that the graph distance $d_{G(n,p}(v,w)>2$ for two fixed vertices $v\ne w$ first, and then sum over all such pairs. Of course, there is a probability p that the two vertices are directly connected by an edge. Then, there are (n-2) other vertices with the potential to be a common neighbour of v and w, which would ensure that the graph distance between them is at most two. So

$\mathbb{P}(d_{G(n,p)}(v,w)>2)=(1-p)[1-p^2]^{n-2} .$

Note that we are using independence throughout this calculation. Then comes the union bound:

$\mathbb{P}(\mathrm{diam}(G(n,p)) >2) \le \sum_{v\ne w \in[n]} \mathbb{P}(d_{G(n,P)}(v,w)>2)$

$\le \binom{n}{2} (1-p)[1-p^2]^{n-2} \rightarrow 0,$

since exponential decay ‘kills’ polynomial growth.

Ultra-sparse regime

In general, we work in the setting where p=p(n) depends on n. If p(n) decays fast enough (see Exercise 2), then with high probability G(n,p) has no edges at all. However, when $p(n)=o(n^{-3/2})$ we have

Proposition: $\mathbb{P}(\text{edges of }G(n,p)\text{ form a matching}) \rightarrow 1$ as $n\rightarrow\infty$ .

A matching is a collection of edges with no vertices in common. So if the edge set of the graph is a matching, we have essentially no interesting connectivity structure at all. The longest path has length one, for example.

To prove this, note that the edge set of the graph fails to be a matching precisely if one of the vertices has degree at least two. But since a vertex v is connected to each of the (n-1) other vertices in the graph independently with probability p, we have

$\mathrm{deg}_{G(n,p)}(v) \sim \mathrm{Bin}(n-1,p),$

and so we can directly make the crude approximation

$\mathbb{P}(\mathrm{deg}_{G(n,p)}(v) =k) = \binom{n-1}{k}p^k(1-p)^{n-1-k}\le n^k p^k.$

We’ve made this very weak bound to make life easier when we sum:

$\mathbb{P}(\mathrm{deg}_{G(n,p)}(v) \ge 2) \le \sum_{k\ge 2}(np)^k = \frac{(np)^2}{1-np}.$

Since $p=o(n^{-3/2})$ , we have $\frac{1}{1-np}=\frac{1}{1-o(1)}=1+o(1)$ , and overall we obtain

$\mathbb{P}(\mathrm{deg}_{G(n,p)}(v) \ge 2) = o(\frac{1}{n}).$

Again, we finish with a union bound, considering this event across all vertices $v\in[n]$ .

$\mathbb{P}(E(G(n,p))\text{ not a matching}) \le \sum_{v\in[n]} \mathbb{P}(\mathrm{deg}_{G(n,p)}(v)\ge 2)$

$=n\mathbb{P}(\mathrm{deg}_{G(n,p)}(1)\ge 2) = o(1),$

as required.

Next time

In the next lecture, we’ll study the regime $p(n)\sim \frac{\log n}{n}$ , where G(n,p) experiences a phase transition from probably not connected to probably connected. Part of this involves making the notion probably connected precise, which will be useful throughout the rest of the course, as well as establishing the language for comparing G(n,p) and G(n,q).

The proof itself requires some more sophisticated versions of calculations from Lecture 1, and more sophisticated probabilistic tools (first- and second-moment methods) to convert them into statements about convergence in probability. This will be an advertisement for the more classical enumerative methods that underpinned much of the early work on random graphs.

The rest of the course will exploit much more some comparisons and embeddings involving branching processes and exploration processes, so don’t worry – it won’t be 26 hours of counting trees!

Kernels of critical graph components

Posted on November 9, 2017 by dominicyeo

This post is motivated by G(N,p), the classical Erdos-Renyi random graph, specifically its critical window, when 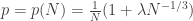$p=p(N)=\frac{1}{N}(1+\lambda N^{-1/3})$ .

We start with the following observation, which makes no restriction on p. Suppose a component of G(N,p) is a tree. Then, the graph geometry of this component is that of a uniform random tree on the appropriate number of vertices. This is deliberately informal. To be formal, we’d have to say “condition on a particular subset of vertices forming a tree-component” and so on. But the formality is broadly irrelevant, because at the level of metric scaling limits, if we want to describe the structure of a tree component, it doesn’t matter whether it has $\log N$ or $\frac{1}{7}N$ vertices, because in both cases the tree structure is uniform. The only thing that changes is the scaling factor.

In general, when V vertices form a connected component of a graph with E edges, we define the excess to be E-V+1. So the excess is non-negative, and is zero precisely when the component is a tree. I’m reluctant to say that the excess counts the number of cycles in the component, but certainly it quantifies the amount of cyclic structure present. We will sometimes, in a mild abuse of notation, talk about excess edges. But note that for a connected component with positive excess, there is a priori no way to select which edges would be the excess edges. In a graph process, or when there is some underlying exploration of the component, there sometimes might be a canonical way to classify the excess edges, though it’s worth remarking that the risk of size-biasing errors is always extremely high in this sort of situation.

Returning to the random graph process, as so often there are big changes around criticality. In the subcritical regime, the components are small, and most of them, even the largest with high probability, are trees. In the supercritical regime, the giant component has excess 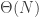$\Theta(N)$ , which is qualitatively very different.

It feels like every talk I’ve ever given has begun with an exposition of Aldous’s seminal paper [Al97] giving a distributional scaling limit of the sizes of critical components in the critical window, and a relation between the process on this time-scale and the multiplicative coalescent. And it remains relevant here, because the breadth-first exploration process can also be used to track the number of excess edges.

In a breadth-first exploration, we have a stack of vertices we are waiting to explore. We pick one and look its neighbours restricted to the rest of the graph, that is without the vertices we have already fully explored, and also without the other vertices in the stack. That’s the easiest way to handle the total component size. But we can simultaneously track how many times we would have joined to a neighbour within the stack, which leads to an excess edge, and Aldous derives a joint distributional scaling limit for the sizes of the critical components and their excesses. (Note that in this case, there is a canonical notion of excess edge, but it depends not just on the graph structure, but also on the extra randomness of the ordering within the breadth-first search.)

Roughly speaking, we consider the reflected exploration process, and its scaling limit, which is a reflected parabolically-drifting Brownian motion (though the details of this are not important at this level of exposition, except that it’s a well-behaved non-negative process that hits zero often). The component sizes are given by the widths of the excursions above zero, scaled up in a factor $N^{1/3}$ . Then conditional on the shape of the excursion, the excess is Poisson with parameter the area under the excursion, with no rescaling. 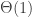That is, a critical component has $\Theta(1)$ excess.

So, with Aldous’s result in the background, when we ask about the metric structure of these critical components, we are really asking: “what does a uniformly-chosen connected component with fixed excess look like when the number of vertices grows?”

I’ll try to keep notation light, but let’s say T(n,k) is a uniform choice from connected graphs on n vertices with excess k.

[Note, the separation of N and n is deliberate, because in the critical window, the connected components have size $n = \Theta(N^{2/3})$ , so I want to distinguish the two problems.]

In this post, we will mainly address the question: “what does the cycle structure of T(n,k) look like for large n?” When k=0, we have a uniform tree, and the convergence of this to the Brownian CRT is now well-known [CRT2, LeGall]. We hope for results with a similar flavour for positive excess k.

2-cores and kernels

First, we have to give a precise statement of what it means to study just the cycle structure of a connected component. From now on I will assume we are always working with a connected graph.

There are several equivalent definitions of the 2-core C(G) of a graph G:

When the excess is positive, there are some cycles. The 2-core is the union of all edges which form part of some cycle, and any edges which lie on a path between two edges which both form part of some cycle.
C(G) is the maximal induced subgraph where all degrees are at least two.
If you remove all the leaves from the graph, then all the leaves from the remaining graph, and continue, the 2-core is the state you arrive at where there are no leaves.

It’s very helpful to think of the overall structure of the graph as consisting of the 2-core, with pendant trees ‘hanging off’ the 2-core. That is, we can view every vertex of the 2-core as the root of a (possibly size 1) tree. This is particular clear if we remove all the edges of the 2-core from the graph. What remains is a forest, with one tree for each vertex of the 2-core.

In general, the k-core is the maximal induced subgraph where all degrees are at least k. The core is generally taken to be something rather different. For this post (and any immediate sequels) I will never refer to the k-core for k>2, and certainly not to the traditional core. So I write ‘core’ for ‘2-core’.

As you can see in the diagram, the core consists of lots of paths, and topologically, the lengths of these paths are redundant. So we will often consider instead the kernel, K(G), which is constructed by taking the core and contracting all the paths between vertices of degree greater than 2. The resulting graph has minimal degree at least three. So far we’ve made no comment about the simplicity of the original graphs, but certainly the kernel need not be simple. It will regularly have loops and multiple edges. The kernel of the graph and core in the previous diagram is therefore this:

Kernels of critical components

To recap, we can deconstruct a connected graph as follows. It has a kernel, and each edge of the kernel is a path length of some length in the core. The rest of the graph consists of trees hanging off from the core vertices.

For now, we ask about the distribution of the kernel of a T(n,K). You might notice that the case k=1 is slightly awkward, as when the core consists of a single cycle, it’s somewhat ambiguous how to define the kernel. Everything we do is easily fixable for k=1, but rather than carry separate cases, we handle the case 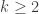$k\ge 2$ .

We first observe that fixing k doesn’t confirm the number of vertices or edges in the kernel. For example, both of the following pictures could correspond to k=3:

However, with high probability the kernel is 3-regular, which suddenly makes the previous post relevant. As I said earlier, it can introduce size-biasing errors to add the excess edges one-at-a-time, but these should be constant factor errors, not scaling errors. So imagine the core of a large graph with excess k=2. For the sake of argument, assume the kernel has the dumbbell / handcuffs shape. Now add an extra edge somewhere. It’s asymptotically very unlikely that this is incident to one of the two vertices with degree three in the core. Note it would need to be incident to both to generate the right-hand picture above. Instead, the core will gain two new vertices of degree three.

Roughly equivalently, once the size of the core is fixed (and large) we have to make a uniform choice from connected graphs of this size where almost every vertex has degree 2, and 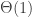$\Theta(1)$ of the rest have degree 3 or higher. But the sum of the degrees is fixed, because the excess is fixed. If there are n vertices in the core, then there are $\Theta(n)$ more graphs where all the vertices have degree 2 or 3, than graphs where a vertex has degree at least 4. Let’s state this formally.

Proposition: The kernel of a uniform graph with n vertices and excess 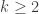$k\ge 2$ is, with high probability as $n\rightarrow\infty$ , 3-regular.

This proved rather more formally as part of Theorem 7 of [JKLP], essentially as a corollary after some very comprehensive generating function setup; and in [LPW] with a more direct computation.

In the previous post, we introduced the configuration model as a method for constructing regular graphs (or any graphs with fixed degree sequence). We observe that, conditional on the event that the resulting graph is simple, it is in fact uniformly-distributed among simple graphs. When the graph is allowed to be a multigraph, this is no longer true. However, in many circumstances, as remarked in (1.1) of [JKLP], for most applications the configuration model measure on multigraphs is the most natural.

Given a 3-regular labelled multigraph H with 2(k-1) vertices and 3(k-1) edges, and K a uniform choice from the configuration model with these parameters, we have

$\mathbb{P}\left( K \equiv H \right) \propto \left(2^{t(H)} \prod_{e\in E(H)} \mathrm{mult}(e)! \right)^{-1},$

where t(H) is the number of loops in H, and mult(e) the multiplicity of an edge e. This might seem initially counter-intuitive, because it looks we are biasing against graphs with multiple edges, when perhaps our intuition is that because there are more ways to form a set of multiple edges we should bias in favour of it.

I think it’s most helpful to look at a diagram of a multigraph as shown, and ask how to assign stubs to edges. At a vertex with degree three, all stub assignments are different, that is 3!=6 possibilities. At the multiple edge, however, we care which stubs match with which stubs, but we don’t care about the order within the multi-edge. Alternatively, there are three choices of how to divide each vertex’s stubs into (2 for the multi-edge, 1 for the rest), and then two choices for how to match up the multi-edge stubs, ie 18 in total = 36/2, and a discount factor of 2.

We mention this because in fact K(T(n,k)) converges in distribution to this uniform configuration model. Once you know that K(T(n,k)) is with high probability 3-regular, then again it’s probably easiest to think about the core, indeed you might as well condition on its total size and number of degree 3 vertices. It’s then not hard to convince yourself that a uniform choice induces a uniform choice of kernel. Again, let’s state that as a proposition.

Proposition: For any H a 3-regular labelled multigraph H with 2(k-1) vertices and 3(k-1) edges as before,

$\lim_{n\rightarrow\infty}\mathbb{P}\left( K(T(n,k)) \equiv H \right) \propto \left(2^{t(H)} \prod_{e\in E(H)} \mathrm{mult}(e)! \right)^{-1}.$

As we said before, the kernel describes the topology of the core. To reconstruct the graph, we need to know the lengths in the core, and then how to glue pendant trees onto the core. But this final stage depends on k only through the total length of paths in the core. Given that information, it’s a combinatorial problem, and while I’m not claiming it’s easy, it’s essentially the same as for the case with k=1, and is worth treating separately.

It is worth clarifying a couple of things first though. Even the outline of methods above relies on the fact that the size of the core diverges as n grows. Again, the heuristic is that up to size-biasing errors, T(n,k) looks like a uniform tree with some uniformly-chosen extra edges. But distances in T(n,k) scale like 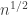$n^{1/2}$ (and thus in critical components of G(N,p) scale like $N^{1/3}$ ). 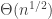And the core will be roughly the set of edges on paths between the uniformly-chosen pairs of vertices, and so will also have length $\Theta(n^{1/2})$ .

Once you have conditioned on the kernel structure, and the (large) number of internal vertices on paths in the core (ie the length of the core), it is natural that the assignment of the degree-2 vertices to core paths / kernel edges is uniform. A consequence of this is that if you record 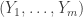$(Y_1,\ldots,Y_m)$ the lengths of paths in the core, where m=3(k-1), then

$\frac{(Y_1,\ldots,Y_m)}{\sum Y_i} \stackrel{d}\rightarrow \mathrm{Dirichlet}(1,1,\ldots,1).$

This is stated formally as Corollary 7 b) of [ABG09]. It’s worth noting that this confirms that the lengths of core paths are bounded in probability away from zero after the appropriate rescaling. In seeking a metric scaling limit, this is convenient as it means there’s so danger that two of the degree-3 vertices end up in ‘the same place’ in the scaling limit object.

To recap, the only missing ingredients now to give a complete limiting metric description of T(n,k) are 1) a distributional limit of the total core length; 2) some appropriate description of set of pendant trees conditional on the size of the pendant forest. [ABG09] show the first of these. As remarked before, all the content of the second of these is encoded in the unicyclic k=1 case, which I have written about before, albeit slightly sketchily, here. (Note that in that post we get around size-biasing by counting a slightly different object, namely unicyclic graphs with an identified cyclic edge.)

However, [ABG09] also propose an alternative construction, which you can think of as glueing CRTs directly onto the stubs of the kernel (with the same distribution as before). The proof that this construction works isn’t as painful as one might fear, and allows a lot of the other metric distributional results to be read off as corollaries.

References

[ABG09] – Addario-Berry, Broutin, Goldschmidt – Critical random graphs: limiting constructions and distributional properties

[CRT2] – Aldous – The continuum random tree: II

[Al97] – Aldous – Brownian excursions, critical random graphs and the multiplicative coalescent

[JKLP] – Janson, Knuth, Luczak, Pittel – The birth of the giant component

[LeGall] – Le Gall – Random trees and applications

[LPW] – Luczak, Pittel, Wierman – The structure of a random graph at the point of the phase transition

Eventually Almost Everywhere

A blog about probability and olympiads by Dominic Yeo

Category Archives: Random Graphs

Lecture 8 – Bounds in the critical window

Lecture 10 – the configuration model

Lecture 9 – Inhomogeneous random graphs

Lecture 7 – The giant component

Lecture 6 – Local limits

Lecture 4 – Hitting time theorem

Lecture 3 – Couplings, comparing distributions

Lecture 2 – Connectivity threshold

Random Graphs – Lecture 1

Kernels of critical graph components